Vol. 3/1 | 2020 | Crappier (en)

A dozen testimonials about the Akan ponderal system, between the beginning of the 17^th century and the end of the 19^th, mention taku (and /or damma), and sometimes a double system of weight, but probably report just that what the Akan showed them. Weak system against portuguese weights, strong system against dutch and english weights, then again weak system at the end of the 19^th century when the gold dust became scarce and of less good quality. The founding role of mitqal is also questioned in favor of a likely coincidence between the Arab and Akan weight systems. In addition, the value of 4.4 g attributed to it would not have been established in the context of the trans-Saharan trade, but later after the arrival of the Europeans, to adapt to their weights.

Keywords: akan - ashanti - baule - gold weight (goldweight, goldgewitch) - Ghana - Côte d'Ivoire - Gold Coast - dualistic system - ethnomathematics - Timothy Garrard - Henry Abel - taku - ba - mitqal - proto-currency

Du début du 17^e à la fin du 19^e siècle, une douzaine de témoignages font état du rôle que tenaient les graines de taku et/ou du damma dans le système pondéral des Akan, et parfois d'un double système poids-faibles/poids forts. Ils n'en rapportent cependant que ce que les Akan en montraient, système faible avec les Portugais, système fort avec les Hollandais et les Anglais, puis à nouveau système faible à la fin du 19^e siècle quand la qualité de la poudre d'or eut baissé. Le rôle fondateur du mitqal est par ailleurs remis en question au profit d'une convergence entre les systèmes pondéraux arabes et akan. De plus, la valeur de 4,4 g qui lui est attribuée ne se serait pas établie dans le cadre de la traite transsaharienne, mais plus tardivement après l'arrivée des Européens, pour s'adapter aux poids de ces derniers.

Mots clés : akan - ashanti - baoulé - poids à peser l'or - Ghana - Côte d'Ivoire - Gold Coast - système dualiste - ethno-mathématiques - Timothy Garrard - Henry Abel - taku - ba - mitqal - proto-monnaie

Introduction

This article is the third in our series on the study of Akan gold weights. In our princeps publication (Crappier et al., 2019), we showed, by studying the largest collection of geometric weights ever studied (9031 including 298 head weights over 80 g) that the Akan weighing system (AWS) was of African origin. But our demonstration, which is based only on metrological arguments, goes against the thesis of Timothy Garrard (Garrard, 1980), which derives it from the Arab weight system, on historical and ethnological arguments and some archaeological clues, which is the authoritative thesis. So we looked at historical sources to see what they could tell us that was different about the origin of the AWS.

Taku story

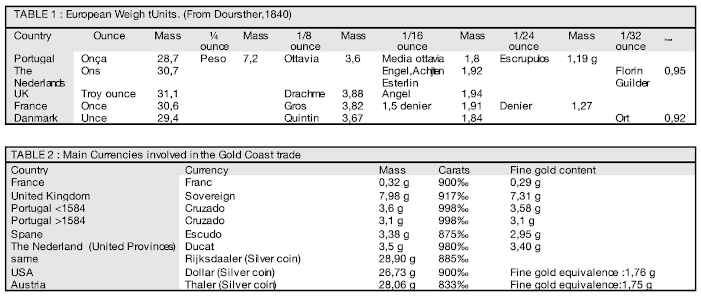
The question of the nature and the mass of taku is the central problem of our investigation of the Akan Weighing System (AWS). Has it varied over centuries, places or witnesses? Are there several taku? A heavy and a light? Jointly or separately? What seeds corresponded to him? Did taku even really exist?

What do the sources say about this?

Method

To answer these questions, we looked for testimonies, accumulated since the 17^th century, from Dutch, English, French, German and Swiss informants. We present them in chronological order, distinguishing between first-hand accounts, when we have been able to access the source document, and second-hand accounts, when they are reported by modern authors. We only retained from these authors the direct or indirect information on the seeds, as well as those which report a double system of weights (dualism). We will then wonder about the mitqal, of which Garrard made the cornerstone of the AWS by taking up his reasoning step by step. Akan units will be noted with our usual abbreviations:

Light taku (≈ 0.22 g) noted T, heavy taku (≈ 0.25 g) noted T*.
Light Ake (≈ 1.76 g) noted A, heavy ake (≈ 2 g) noted A*.
Light Ba (≈ 0.146 g) noted B, ba (≈ 0.166 g) noted B*.

The main weights and currencies of Europeans involved in Akan gold trade are listed in table 1 and 2 (Annex)

Results

 The taku exists. Most witnesses state it, whether or not associated with damma.

1602. De Marees:
The oldest testimony that we have found is that of Pieter de Marees. Dating from 1602, we consulted it on the Gallica base in a French translation of 1605. At that time Portugal was the dominant power on the Gold Coast and, although Dutch, de Marees gives its information in pesos and refers to the Portuguese ounce. However, this list seems marred by a few errors that Garrard corrected. The main information we get from this is that the benda is worth 2 ounces, or 57.4 g. He does not speak of taku, but of red and black seeds that Africans use and of which they know the value, without indicating the latter. We also learn that agiraotwe is worth ½ peso, or 3.6 g and therefore that agiraotwe-fa, which corresponds to ake, weighs 1.8 g. We are in the light system (de Marees, 1605).

1668. Dapper:
The following testimony is that of Olfert Dapper in 1668. Second hand testimony since Dapper, who has never set foot in Africa, uses a source which has been lost. A French translation of his work dating from 1685 can be found on Gallica, but the list of Akan weights it contains is incorrect because it has been shifted by one line. Garrard provided an exact version. Dapper theoretically refers to the Dutch troy ounce in which 1 engel weighs 1.92 g and is worth 2 guilders but on closer inspection it can be seen that, if the name correspondence with the heavy system is valid up to at 3 engels, everything goes wrong from 10 engels, where the weights can correspond to the theoretical values only in the light system. This is a clue in favor of dualism, especially since Dapper would report, according to Garrard because we do not find any trace of it in the French edition, that the people of Accra used 2 distinct series of weights, the one light, the other heavy (Dapper, 1686).

1676. Muller:
Hamburg merchant, Wilhelm Johann Muller published in 1676 a very detailed list of the weights used by the Fanti. He is the first to speak of damma and taku, without describing them. However, we can calculate the mass of the taku that he gives for 1/6 of a guilder, i.e. 0.16 g. In our terminology, this means B*. This list is therefore drawn up in heavy weights (Muller, 1676).

1678. Barbot:
Jean Barbot, French trader for the Senegal company, tells us in 1678 that the inhabitants of Accra “commonly used two kinds of weight for gold, one heavier than the other, and divided proportionally so that each (ounce) contains 16 angels or acke, and bargained between them to pay with the heaviest or the lightest, which is an exact description of the dualistic system and how to use it (Debien, 1979).

1704. Bosman:
Willem Bosman is a Dutch merchant who wrote in 1704 and uses the 30.7 g Dutch troy ounce. He cites damba, a small red bean encrusted with black, 24 of which make a gold esterlin (1.92 g), but also other seeds, some of which are white, encrusted with black, sometimes even all black, called tacoe and weighing a little more than double the damba. He thus describes a damma seed (Abrus precatorius) of 0.08 g, two of which make a B* of 0.16 g (and three of 0.24 g a T*), and perhaps also the seed of nere (Parkia biglobosa), beige and black when it is in her cuticle, black when she has been rid of it. We are in the heavy system (Bosman, 1705).

1817. Bowdich:
Thomas Bowdich is English. His book is one of our main sources of information on the Ashanti, with whom he stayed as ambassador in 1817. He tells us that at the time an English troy ounce of 31.1 g of Akan gold was worth £ 4. (or 7.8g for £ 1 ¹) or 16 ackie. The ake therefore worth 1.94 g. We are in the heavy system. He also tells us, somewhat cryptically that “8 tokoos (a small berry) are reckoned to the ackie, but it will not weight more than seven” which means that its tokoo weighed 1.94 / 8 ≈ 0.24 g (T*) and which suggests that there was also a lighter ake weighing "no more than seven” tokoos, ≈ 1.70 g and opens the door to the dualistic system (Bowdich, 1819).

1848. Bouët-Willaumez :
In the account of his exploration of the western coasts of Africa, this future French admiral tells us, page 110, that the currency in Gold Coast, from Grand Bassam, is the acquêt, which is worth 5.60 f , or 1.84 g at the local rate of 3 f per gram of gold. On page 115, he tells about a golden takon, used in Elmina, the mass of which is 1/16 of gros, or 0.24 g. We will recognize ake and taku in their heavy version. (Bouët-Willaumez, 1848).

1852. MacLean, 1868; Horton, 1868, quoted by Garrard: 
English governor of fort from 1830 to 1847, MacLean published a list of weights in both ozt and pound, which Garrard reports on page 256 when translating it to grams. MacLean mentions among the Ashanti a damma of 0.074 g, a takufan (half-taku) of 0.11 g but also a taku of 0.26 g as well as sul (suru) of 8.8 g, which must correspond to 1 £. The value of the damma corresponds to that of the light ba, and the values given for taku to a T of 0.22 g and a T* of 0.26 g. He also mentions in a list of Fanti weights a taku of 0.33 g which corresponds to a taku of 9 pence (p) which seems to have existed among the Fanti, and which we find later in a list collected by Garrard (page 341).
Garrard, however, reports a contradictory information which he found in Horton (1868) which gives this 9 p weight, still in Fanti country, the name of teycoo na simpoir. Simpoir (sempowa) being worth 3 p, we fall back in facts on the taku of 6 p. Horton also cites this 6 p teycoo, as well as an archi of $ 1, equal to 4 s 6 d. One could not better describe a T of 0.22 g and 1 A* of 1.95 g, which again refers to the dualistic system (Garrard, 1980).

1874. Bonnat; 1875. Kuhne et Ramseyer, quoted by Menzel:
Marie-Joseph Bonnat, a French merchant, was hostage to the Ashanti from 1869 to 1874. His notes have been published in 1994. He described at length the Ashanti society.
Swiss missionaries Kuehne and Ramseyer, as well as Mrs. Ramseyer, shared this captivity and made an independent account of it.
Although provided with gold and weight for his daily life by his forced hosts, Bonnat did not detail how it worked. He teaches us however over the pages that 6 tacous are worth 4.80 F, (page 327), that 2 periguans are worth $72, (page 405), and that 20 periguans weigh 45 ounces (of 32 g ²) (page 396). Bonnat also explains to us how the Ashanti, having exhausted their natural resources of gold dust, went about making it from nuggets in order to ensure their monetary circulation (Perrot, 1984).
Kuehne for his part reports a detailed list of Ashanti weights with their correspondence in dakoo and dollars which tells us that one US dollar is worth 8 dakoo and that $16 are worth one ounce of gold powder. At the coast, in Fanti country, this ounce is worth £ 3 12, one dollar is worth 1 ackie and a pereguin is counted for $ 36 (Menzel 1968).
From this information, we retain from Bonnat, that a tacou which is worth 80 cents weighs 1/3 g x 0.80 = 0.26 g and that a periguan weighs 2.25 ozt, or 72 g, the mass that Zeller gives to it ³.
We also note that for Kuehne the dollar corresponds to 1.95 g of Akan gold, that the dakoo weighs 0.243 g and that the pereguin weighs 70.2 g.
Although Bonnat values the taku too high, these data are consistent with the heavyweight system.

1875. Christaller :
Johann Christaller, German missionary lived from 1853 to 1868 in Ghana. He is one of the first translators of Twi, the language of the Akan. According to Zeller, he reports a double system of weights and also of scales, different for buying or selling (Zeller, 1913).

1889. Binger :
Between 1887 and 1889 Captain Binger explored Africa from west of Niger to the Gulf of Guinea. He is the last author to document a functioning AWS. He tells us about the current currencies in Salaga (North-East of Kumasi), Bondoukou ⁴.
and in Agni country. Binger uses a 32 g trade ounce, and estimates the gram of akan gold at 3 f, or 0.33 g for 1 franc ⁵.
In Salaga, you pay in cowries but also in metal bars (barifari of 17.6 g). The mitqal is worth 4 g, although 1 barifari is supposed to make 4 mitqal.
In Bondoukou you pay in cowries, but also in seeds and metal weights. The smallest seed, the damma, is worth 2.25 f and therefore weighs 0.075 g which corresponds to low weights.
Here the barifari also weighs 16 g and the mitqal 4 g. Binger also notes that the small weights are too heavy and that the merchants buy gold from prospectors with heavy weights, and resell it to the Ashanti with low weights.
In Agni country in the south-east of the Ivory Coast, cowries are no longer used. Binger draws up a very complete list of Agni weights, with their equivalents in gold francs. We retain for our purposes that the ounce is worth 16 ake at 6 fr, that each ake is worth 12 ba (sometimes called tacou) at 50 cents and that the damma is worth 0.25 fr. The barifari weighs 16 g. A damma weighs 0.082 g, and a taku weighs 0.164 g, which is actually B*. We therefore have a barifari which varies from 17.6 g to 16 g, which Binger explains by imprecision and wear, and a damma which varies from 0.075 g to 0.082 g which again lays the foundations for a dualistic system.
Note that 3 Binger ba at 50 c are worth about 2 Bonnat tacou at 80 c, in the usual ratio of 3 to 2 between these two units (Binger, 1892).

After 1900. Garrard and Abel:
Abel’s information was gathered in 1952 from the Agni, Baule and Aboure. None of the notables interviewed, even the older ones, knew how to use weights, but most remembered the existence of male and female weights (Abel, 1973).
Garrard reports 12 lists from informants of different Akan states. The oldest was born in 1872. The values are given in English currency. They are calculated at 3 £ 12 s per ounce, so in the light system, with a taku at 6 p, or 0.22 g. None of them remembers the existence of male and female weights, nor does he ever mention the name of the mitqal (Garrard, 1980).

Discussion

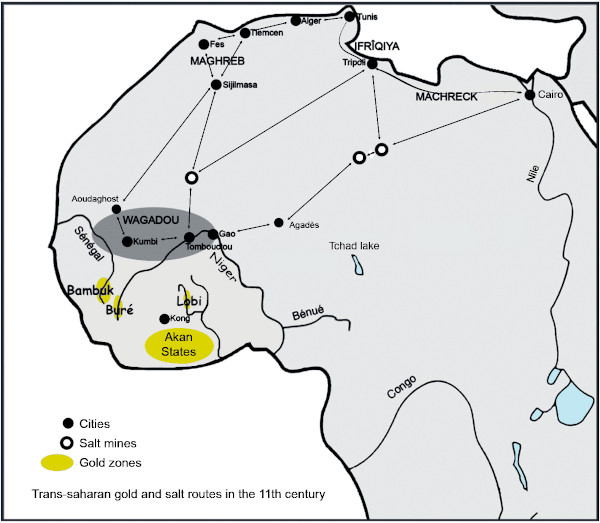
Out of 12 recorded testimonies, only 3 make no mention of the seeds, those of Dapper and Barbot, and that of Bouet (who however quotes the takon) but all speak of ake, as 1/16 of an ounce. Dapper, Barbot and Binger directly point to a dualistic system, which is also reflected in the inconsistencies of the other lists. We are in fact in the presence of two closed systems, which communicate only through commercial transactions. The Akan system on the one hand, the European system on the other. Akan operate at constant price and variable weight, Europeans at constant weight and variable price. We only have information on the first through the second.

On the one hand, are internal transactions between Akan through the exchange of gold dust. Regardless of its purity they are not able to assess it with precision. Once the quality of the gold is deemed acceptable by both parties, only counts the difference between the weight of the buyers and the weight of the sellers. For the retail trade which makes the bulk of sales between Akan, they use the small weights ⁶. For wholesale trade with Europeans, Akan merchants use the highest values, benda or beyond, using those of their weights which correspond to those of their interlocutors.

On the other hand, the Europeans. We will choose the English because they are the ones on which we are the best documented. Their currency, the Sovereign, is stabilized since 1816 at 8 g of gold at 916 ‰ (22 carats) or 7.32 g of fine gold. Their aim is to acquire gold in exchange of goods which they have paid for in £ to their suppliers. They calculate their profit in that currency, taking in account the purity of the gold ore they get as payment. They weigh it in troy ounces, with their scales and weights, but they cannot impose their weighings because their interlocutors are able to verify the transactions with their own apparatus. It is on this occasion that information on the respective weight systems is exchanged. Each European therefore only needs to know the part of the Akan system that corresponds to his weights.

If we can easily understand that the transactions were made with the Portuguese in the light system (onça of 28.7 g), then with the Dutch and the English in the heavy one (troy ounce of 30.6 and 31.1 g), It remains to be explained why in the last quarter of the 19th century the light system was again resorted to. Things happens as if Akan gold had been devalued from 925 ‰ (22.2 carats) to 800 ‰ (19.2 carats) which can be explained by the rarefaction of natural gold dust, the purity of which exceeds 22 carats, and its replacement by nuggets, of lesser grade, or artificial powder as the Ashanti knew how to make. It is therefore difficult to understand why the conversions would have been made in the first case in the heavy system, and in the second in the light system. The reverse seems more logical, the Akan buyer having to donate more gold to get the same product from the English merchant. To understand, let's analyze the sale of a trade gun.

In 1820, the price of a Brown Bess rifle ⁷ was around £ 1. With an ozt of gold having a buying power of £ 4, it takes 7.8 g for £ 1. The Akan buyer had to pay 4 A* at 1.95 g or 32 T* at 0.24 g. The transaction was therefore done in the heavy system. In 1870, an ozt of gold had a purchasing power of only 3 £ 12 s, it took 8.8 g for 1 £. For the Akan buyer this amount corresponds to 5 A of 1.76 g or 40 T of 0.22 g. The transaction was then done for him in the light system. The switch from one system to another was therefore done simply, without the English trader realizing it and therefore not being able to report it.

Conclusion

Our original article had highlighted the duality of the weights, but without being able to affirm, because of the heterogeneity in time and space of the collection on which our study concerned, that it was an integrated system weight to sell / weight to buy. This analysis of the sources confirms the plausibility of this dualist theory, which is, on reflection, more than the weight of the taku, the essential point of the Akan Weight System.

Mitqal story

What about the mitqal which Zeller claims to be not used in the Gold Coast, but which Garrard makes the cornerstone of the AWS. Could it be, like the weights corresponding to European weights, just one of the many facets of the Akan system, used in trade with North Africa?

Let us summarize Garrard's thesis

In the year 600, the weights and coins in use in the Mediterranean and Middle Eastern worlds were those of the Byzantines, inherited from the Romans, and those of the Persians, a distant heritage of the Greeks of Alexander the Great. Fifty years later, after having conquered a large part of these empires, the Arabs merged these Persian and Byzantine currencies into their bimetallic system. From the first they adopt the drachme, a silver coin which they make their dirhem, from the second the denarius aureus, a gold coin which they make their dinar. For weighing, they keep the Roman weight units in use. The 27.3 g uncia takes the name uqiya and the sextula, its sixth becomes the mitqal, which gives it the mass of 4.55 g. Weights and currencies meet at the level of the dinar and the mitqal ⁸, two terms that will end up meaning the same thing. This system reaches the Sahel via the Sahara, then the Akan, at the same time as the process of manufacturing the weights. The Akan would thus have imported a system based on the mitqal with as proof the discovery of very old weights, in terracotta, to this standard. They would then have adapted to European weights, as the Portuguese, Dutch and English arrived on the Gulf of Guinea coasts. Garrard, after a very documented historical account on the dinar, but ultimately unrelated to his conclusion, tells us that it would be this uqiya of 27.3 g, reduced, he does not say why, at 26.4 g, divisible into six 4.4 g mitqal and the so-called trading ounce, which is said to have been used in Sudan ⁹ for the gold trade ¹⁰.

Discussion

The problem is that we have not found a trace of a 4.40 g dinar or mitqal at any time in a North African country involved in the trans-Saharan trade. In Egypt, the starting point of the eastern caravans, the dinar, around 1200, weighs 4 g. In Morocco, where the northern come from, its nominal weight varies from 4.25 g around 1050 to 4.72 g around 1130 (see framed text and map).

To find our way around, let's see schematically the course of an ounce of gold versus that of a load of salt around 1150, a date on which the Akan were probably already integrated into the trans-Saharan trade as gold producers:
- In the north, the Berbers of Morocco control the salt mines in the Sahara. They use dinars among themselves, the mass of which they can control with the corresponding mitqal, but which in their trade with Sudan is only a unit of account whose cash does not circulate ¹¹. At that time, they count in Almohad dinars of 4.7 g. They use monetary weights of glass or brass to weigh the gold which they exchange for salt. Their dinars have a purity of 23 carats.
- In the south, Akan people, who domesticated the forest and about whom we do not know much in this time. We will assume that they already use gold dust as currency and that they weigh it with damma or taku seeds in their dualistic system. They have gold, but no salt.
- Between them the Dioula. This caste of Islamized Soninke merchants monopolizes trade along the Niger, where the northern caravans end in Timbuktu. They exchange salt for gold, dust or nuggets. Transactions are done in mitqal. They learn from Berbers how to handle weights and how to make them themselves using lost wax. They then trade salt for gold in production areas, the closest of which are Bambuk in Senegal and Bure in Guinea. This barter is sometimes done there silently ¹², at least without weighing goods, depending on supply and demand, and probably regulated by traditional criteria. These deposits being exhausted, the Dioula venture further south, to the edge of the forest where they founded, around 1050 according to Binger, the city of Kong in contact with the Akan, with whom gold is not simply bartered by esteem, but weighed. Of all the gold producers frequented by the Dioula, they are the only ones with whom this has happened. It makes sense if you admit that they already had their own weighing system in which the mitqal found itself in phase with an Akan weight.

If this weight is nso-nsa (that is to say 7x3), the name that has come down to us, and if we keep at taku the value of 0.22 g in the light system, its value would have been 0.22 x 21 = 4, 6 g, which corresponds to an Almohad dinar with almost parity of purity, which is quite likely because Akan gold was considered very pure. So, how can we explain that nso-nsa, in every list of weights that we have studied, is given for 20 taku, a value which in our terminology should have been called nun-nan (5x4)?

7x3 = 20 or the crossroads of worlds

Let's go back to our reasoning:
We are now at the end of the 15^th century. Exchanges between Akan and Dioula are always done on the basis of a mitqal of 4.72 g, or 21 taku in the weak system. These mitqals are measured with monetary weights of brass that the Akan have learned to make. They adopted for their foreign trade this unit, widely used in the Mediterranean world and well known to Portuguese sailors with whom they have just started to trade.

The Portuguese use as a unit for weighting precious metals onça, in fact the ounce of Cologne, of 28.7 g, which is divided by 4, 8.16 and 32 but also by 24 which corresponds to one escrupulos of 1.16 g (Doursther, 1840). Four of these escrupulos weigh 4.64 g, exactly nso-nsa. As a result of this coincidence, the Akan would have had nothing to change in their habits to control the weighings of the Portuguese if they had, like the Dioula, used monetary weights. But, because it is easier when traveling, they used nested cup weights, each of which weighs half the previous one (see the detail of the painting by Quentin Metsys), with which it is therefore not possible to weigh 1/6 of ounce. You can only approximate it, by adding two cups of 1/8 and 1/32 = 5/32 (≈ 4,5 g).

If we admit that they exchanged in mitqal, a unit known to both parties, the Akan, to adapt, went from their multiples by 3, 6, 12 ... to those by 2, 4, 8 ... and therefore from nso-nsa to nun-nan. The difference was small and from their point of view, it was a gain. As for the Portuguese, Akan gold was such a boon to them that, even if they had been aware of this subtlety, they would not have cared..

When, why and how did the confusion of names occur between the weight used with the Dioula and its surrogate with the Portuguese? We will never know, but we understand that through mixing, recombination and approximation, this semantic shift has occurred over the centuries. This mathematical incongruity would thus be the trace of the entry of the Akan into the first globalization, the crossroads of the European and African worlds.

Conclusion

Thing are going as if the diversity of their weights has allowed the Akan to adapt to the Arab system in the same way they would later adapt to European systems. The mitqal would only be a guest, not the basement. As we progress in our investigation, the image of an autonomous and indigenous AWS becomes increasingly clear. However, it is difficult to think that it could have been born in the heart of the forest for the simple reason that there were no metals suitable for the manufacture of scales, without which weighing, even in seeds, could not have been possible. The Akan claim to be the descendants of the Wagadou ¹³, empire, a legend of which we do not know the part of the truth. Scales and weights were known there for the gold trade, which was already done with North Africa, and Abrus precatorius, whose red and black seeds make damma, as well as Parkia biglobosa, which the black seeds may be the taku, were growing there. The interpenetration between the Arab metal system and the African grain system was therefore able to take place there, before the Akan migrate south, towards the forest, to escape the Islamization imposed by the Almoravids.

References

Ben Rhombdane K., 1979. Supplément au catalogue des monnaies musulmanes de la Bibliothèque nationale: monnaies almoravides et almohades. Revue Numismatique, 21: 141-175.

Binger L. G., 1892. Du Niger au Golfe de Guinée par le pays de Kong et le Mossi. Paris, Hachette, 2 vol. (vol. premier, 513 p.; vol. second, 414 p.).

Bosman W., 1705. A new and accurate description of the coast of Guinea, divided into the Gold, the Slave, and the Ivory coasts. London, Ballantyne Press, 512 p. [Ed. Frank Cass, 1967].

Bouët-Willaumez L.-E., 1848. Commerce et traite des noirs aux côtes occidentales d'Afrique. Paris, Imprimerie Nationale, 230 p.

Bowdich T. E., 1819. Mission from Cape Coast Castle to Ashantee, with a statistical account of that kingdom, and geographical notices of other parts of the Interior of Africa. London, John Murray, 512 p. [Ed. Frank Cass, 1966].

Dapper O., 2007 [1686]. Description de l'Afrique, contenant Les Noms, la Situation & les Confins de toutes ses Parties, leurs Rivières, leurs Villes & leurs Habitations, leurs Plantes & leurs Animaux ; les Mœurs, les Coûtumes, la Langue, les Richesses, la Religion & le Gouvernement de ses Peuples. Avec Des Cartes des Etats, des Provinces & des Villes, & des Figures en Taille-douce, qui représentent les habits & les principales Ceremonies des Habitans, les Plantes & les Animaux les moins connus. Amsterdam, chez Wolfgang, Waesberge, Boom & van Someren, 534 p., 42 pl. http://catalogue.bnf.fr/ark:/12148/cb34554868. Consulté en ligne en septembre 2017.

De Marees P., 1605. Description et récit historial du riche royaume d'or de Gunea (sic), aultrement nommé, la coste d'or de Mina, gisante en certain endroict d'Africque. Amsterdam, chez Cornille Claesson, 100 p. [Les éditions Chapitre.com, 2017]

Debien G., Delafosse M. & Thilmans G., 1979, Journal d'un voyage de traite en Guinée, à Cayenne et aux Antilles fait par Jean Barbot en 1678-1679. Bulletin de l'Institut fondamental d'Afrique noire (série B), 40(2): 235-395.

Doursther H., 1840. Dictionnaire universel des poids et mesures anciens et modernes. Bruxelles, Hayez, 603 p.

Garrard T. F., 1980. Akan weights and the gold trade. Legon history series. London, Longman, 393 p.

Guilhiermoz P., 1906. Note sur les poids du moyen âge (première partie). Bibliothèque de l'école des chartes, 67: 161-233.

Menzel B., 1968. Goldgewichte aus Ghana. Berlin, Museum für völkerkunde, Neue Folge, 12, Abteilung Afrika III, 241 p.

Müller W. J.,1676. Die Afrikanische auf der guineischen Gold-Cust gelegene Landschaft Fetu. Hamburg, Zacharias Härtel (3^e ed.)

Perrot C.-H., van Dantzig A., 1994. Marie-Joseph Bonnat et les Ashanti-Journal (1869-1874). Coll. Mémoires de la Société des Africanistes. Paris, Société des Africanistes, 672 p.

Roux C. & Guerra M.F, 2000. La monnaie Almoravide : de l'Afrique à l'Espagne. ArchéoSciences, revue d'archéométrie, 24: 39-52.

Zeller R., 1913. Die goldgewichte von Asante (westafrika) eine ethnologische Studie. Leipzig, Teubner, 77 p.

Annexe

1. This corresponds to a fine gold grade of 925 ‰, higher than that of a sovereign's gold coin which is 916 ‰. ⇧
   

2. Bonnat probably counts in a 32 g “trade ounce”, a unit used in French counters in Africa. His biographers seem to have been mistaken on this point of detail. ⇧
   

3. For Zeller, the pereguan is worth 288 T* and therefore weighs 72 g. See The Akan multiplication table, table 2. ⇧
   

4. On the border between Ivory Coast and Ghana, east of the Baoulé country. ⇧
   

5. 1 gold Franc weighs 0.32 g at 900 ‰, or 0.29 g of fine gold. The purity of Akan gold is therefore estimated at 878 ‰. ⇧
   

6. Note that a single weighting system is sufficient for direct purchases from producers, then there is no middleman who has his benefit to take. ⇧
   

7. The Brown Bess, or long pattern rifle, the rifle of the English infantry during the Napoleonic wars, was highly prized for its robustness by Africans. Most informants report a price between 3 and 4 A*. ⇧
   

8. Mitqal, in Arabic, would mean mass (Doursther, 1840). ⇧
   

9. In Arabic sudan literally means land of blacks, as opposed to beidan, land of whites (North Africa). ⇧
   

10. There are several inaccuracies in Garrard's book. First, it was not the Arabs who "invented" the dinar, but the Persians, apparently following a confusion of weight and term between silver denarius with a weight of 4.5 g and the aureus, improperly called denarius aureus. Secondly, the weight of Diocletian’s aureus, to which he gives the value of 4.7 g, fluctuates a lot, varying from ≈ 5.6 to ≈ 4.8 g, but being more often> 5.45 g. Finally, the 12^th century Almohad dinar did not weigh 4.5 g, but 4.72 g. These details have little influence on his thesis, since ultimately he only takes into account the Roman ounce of 27 g and its 1/6. ⇧
    

11. It would be absurd to buy gold dust with gold coins. ⇧
    

12. To ensure their safety, the two parts do not meet. The Dioula deposit their salt, the producers deposit a certain amount of gold in exchange, and so on until they come to an agreement. ⇧
    

13. Medieval African Empire better known as the Empire of Ghana. ⇧
    

Jean-Jacques Crappier
MD, Collector, Le Mans, France
Email : Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.