Vol. 3/1 | 2020 | Crappier (fr)

Du début du 17^e à la fin du 19^e siècle, une douzaine de témoignages font état du rôle que tenaient les graines de taku et/ou du damma dans le système pondéral des Akan, et parfois d'un double système poids-faibles/poids forts. Ils n'en rapportent cependant que ce que les Akan en montraient, système faible avec les Portugais, système fort avec les Hollandais et les Anglais, puis à nouveau système faible à la fin du 19^e siècle quand la qualité de la poudre d'or eut baissé. Le rôle fondateur du mitqal est par ailleurs remis en question au profit d'une convergence entre les systèmes pondéraux arabes et akan. De plus, la valeur de 4,4 g qui lui est attribuée ne se serait pas établie dans le cadre de la traite transsaharienne, mais plus tardivement après l'arrivée des Européens, pour s'adapter aux poids de ces derniers.

Mots clés : akan - ashanti - baoulé - poids à peser l'or - Ghana - Côte d'Ivoire - Gold Coast - système dualiste - ethno-mathématiques - Timothy Garrard - Henry Abel - taku - ba - mitqal - proto-monnaie

A dozen testimonials about the Akan ponderal system, between the beginning of the 17^th century and the end of the 19^th, mention taku (and /or damma), and sometimes a double system of weight, but probably report just that what the Akan showed them. Weak system against portuguese weights, strong system against dutch and english weights, then again weak system at the end of the 19^th century when the gold dust became scarce and of less good quality. The founding role of mitqal is also questioned in favor of a likely coincidence between the Arab and Akan weight systems. In addition, the value of 4.4 g attributed to it would not have been established in the context of the trans-Saharan trade, but later after the arrival of the Europeans, to adapt to their weights.

Keywords: akan - ashanti - baule - gold weight (goldweight, goldgewitch) - Ghana - Côte d'Ivoire - Gold Coast - dualistic system - ethnomathematics - Timothy Garrard - Henry Abel - taku - ba - mitqal - proto-currency

Introduction

Cet article est le troisième de notre série consacrée à l'étude des poids à peser l'or des Akan. Dans notre publication princeps (Crappier et al., 2019), nous avons montré, par l'étude de la plus grande collection de poids géométriques jamais étudiée (9031 dont 298 poids de chef de plus de 80 g) que le Système Pondéral Akan (SPA) était d'origine africaine. Mais notre démonstration, qui ne repose que sur des arguments métrologiques, va à l'encontre de la thèse de Timothy Garrard (Garrard, 1980), qui le fait dériver du système pondéral des Arabes, sur des arguments historiques, ethnologiques et quelques indices archéologiques, et qui fait autorité. Nous nous sommes donc penché sur les sources historiques pour voir ce qu'elles pouvaient nous apprendre de différent sur l'origine du SPA.

Histoire de taku

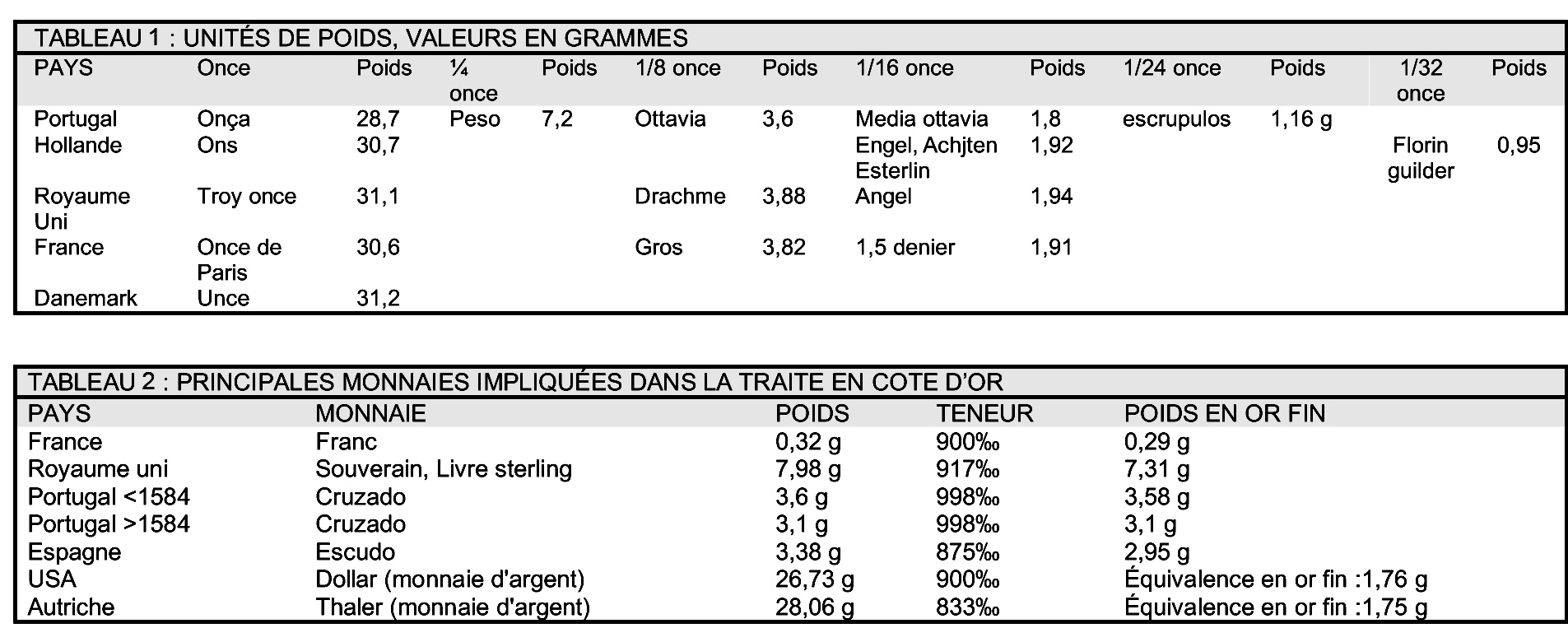
La question de la nature et de la masse du taku est le problème central de notre enquête sur le système pondéral akan. A-t-il varié au gré des siècles, des lieux, des témoins ? Y a-t-il plusieurs taku ? Un fort et un faible ? Conjointement ou séparément ? Quelles graines lui correspondaient ? Le taku a-t-il seulement vraiment existé ?

Que disent les sources à ce propos ?

Méthode

Pour répondre à ces questions, nous avons recherché les témoignages, accumulés depuis le 17^e siècle, d'informateurs hollandais, anglais, français, allemands et suisses. Nous les présentons dans l'ordre chronologique, en distinguant entre témoignages de première main, quand nous avons pu accéder au document source, et témoignages de seconde main, quand ils sont rapportés par des auteurs modernes, en n'en retenant que les informations directes ou indirectes sur les graines, ainsi que celles qui font état d'un double système de poids (dualisme). Nous nous interrogerons ensuite sur le mitqal, dont Garrard fait la pierre angulaire du système pondéral akan en reprenant pas à pas son raisonnement. Les unités akan seront notées avec les abréviations habituelles :

Taku faible (≈ 0,22 g) noté T, taku fort (≈ 0,25 g) noté T*.
Aké faible (≈ 1,76 g) noté A, aké fort (≈ 2 g) noté A*.
Ba faible (≈ 0,146 g) noté B, ba fort (≈ 0,166 g) noté B*.

En annexe figurent les principaux poids et monnaies des Européens engagés dans le commerce avec les Akan (Annexe : tableaux 1 et 2).

Résultats

 Le taku existe. La plupart des témoins l'ont rencontré. Lui ou son petit frère, le damma.

1602. De Marees :
Le plus ancien témoignage que nous ayons retrouvé est celui de Pieter de Marees. Datant de 1602, il est consultable sur Gallica dans une traduction française de 1605. À cette époque le Portugal est la puissance dominante sur la Côte d'or et bien que Hollandais, de Marees donne ses informations en pesos et se réfère à l'once portugaise. Sa liste semble cependant entachée de quelques erreurs que Garrard a corrigées. La principale information qu'on en tire est que le benda vaut 2 onça, soit 57,4 g. Il ne parle pas du taku, mais de graines rouges et noires que les Africains utilisent et dont ils connaissent la valeur, sans indiquer cette dernière. On y apprend aussi que agiraotwe, qui vaut dans le système faible 16 T, vaut ½ peso, soit 3,6 g et donc que agiraotwe-fa, qui correspond à l'aké, pèse 1,8 g. Nous sommes dans le système faible (de Marees, 1605).

1668. Dapper :
Le témoignage suivant est celui de Olfert Dapper en 1668. Témoignage de seconde main puisque Dapper, qui n'a jamais mis les pieds en Afrique, utilise une source qui a été perdue. Une traduction en Français de son ouvrage datant de 1685 est consultable sur Gallica, mais la liste de poids akan qui y figure est erronée car décalée d'un cran. Garrard en fourni une version exacte.
Dapper se réfère théoriquement à l'once troy de Hollande dans laquelle 1 engel pèse 1,92 g et vaut 2 florins (guilder) mais à regarder de plus près, on voit que si la correspondance des noms avec le système fort est valable jusqu'à 3 engels, tout se dérègle à partir de 10 engels où les poids ne peuvent correspondre à des valeurs théoriques que si on passe dans le système faible.
On tient là un indice en faveur du dualisme, d'autant que le même Dapper rapporterait, selon Garrard car on n'en trouve pas trace dans l'édition française, que les gens d'Accra utilisaient deux séries de poids distinctes, l'une légère, l'autre lourde (Dapper, 1686).

1676. Muller :
Sujet Hambourgeois, Wilhelm Johann Muller a publié en 1676 une liste très détaillée des poids utilisés par les Fanti. Il est le premier à parler du damma et du taku, sans les décrire toutefois. On peut néanmoins calculer la masse du taku qu'il donne pour 1/6 de guilder soit 0,16 g. Il s'agit dans notre terminologie du B*. Cette liste est donc établie en poids forts (Muller, 1676).

1678. Barbot :
Jean Barbot, Français trafiquant pour la compagnie du Sénégal nous apprend en 1678 que les habitants d'Accra « utilisaient communément deux sortes de poids pour l'or, l'un plus lourd que l'autre, et divisés proportionnellement pour que chaque (once) contienne 16 angels ou acke, et marchandaient entre eux pour payer avec le plus lourd ou le plus léger ¹ », ce qui est une exacte description du système dualiste et de la façon de l'utiliser (Debien, 1979).

1704. Bosman :
Willem Bosman est un marchand hollandais qui écrit en 1704 et qui utilise l'once troy hollandaise de 30,7 g. Il cite le damba, petite fève rouge marquetée de noir dont 24 font un esterlin d'or soit 1,92 g, mais aussi d'autres graines, dont certaines blanches, marquetées de noir, quelquefois même toutes noires, qu'on appelle tacoe et qui font un peu plus du double. Il décrit par là une graine de damma (Abrus precatorius) de 0,08 g, dont deux font un B* de 0,16 g (et trois un T* de 0,24 g), mais peut être aussi la graine de néré (Parkia biglobosa), beige et noire quand elle est dans sa cuticule, noire quand elle en a été débarrassée. Nous sommes dans le système fort (Bosman, 1705).

1817. Bowdich :
Thomas Bowdich est anglais. Son livre est une de nos principales sources d'information sur les Achanti, chez qui il fut chargé d'une ambassade en 1817. Il nous apprend qu'à l'époque une once troy anglaise de 31,1 g d'or Akan valait 4 £ (soit 7,8 g pour 1 £ ²) ou 16 ackie. L'aké valant donc 1,94 g. Nous sommes dans le système fort.
Il nous dit aussi, de façon un peu sibylline que “8 tokoos (a small berry) are reckoned to the ackie, but it will not weight more than seven”, ce qui veut dire que le tokoo pesait 1,94/8 ≈ 0,24 g (T*) et qui laisse entendre qu'il existait aussi un aké plus léger ne pesant “pas plus que 7 tokoos”, soit ≈ 1,70 g et ouvre la porte au système dualiste (Bowdich, 1819).

1848. Bouët-Willaumez :
Dans le compte rendu de son exploration des côtes occidentales d'Afrique, ce futur amiral français nous dit, page 110, que la monnaie en Côte d'or, à partir de Grand Bassam, est l'acquêt, qui vaut 5,60 f, soit 1,84 g au cours local de 3 f le gramme d'or. Page 115, il cite à Elmina le takon d'or, dont la masse fait 1/16 de gros soit 0,24 g. On reconnaîtra l'aké et le taku dans leur version forte (Bouët-Willaumez, 1848).

1852. MacLean, 1868. Horton, cités par Garrard : 
Gouverneur de forts en Côte d'or de 1830 à 1847, MacLean a publié une liste de poids à la fois en ozt et en £ dont Garrard fait état page 256 en la traduisant en grammes. Il mentionne chez les Ashanti un damma de 0,074 g, un takufan (demi-taku) de 0,11 g mais aussi un taku de 0,26 g ainsi que sul (suru) pour 8,8 g, ce qui doit correspondre à 1 £. La valeur du damma correspond à celle du ba léger, et les valeurs données pour le taku à un T de 0,22 et un T* de 0,26 g. Il mentionne aussi dans une liste de poids fanti un taku de 0,33 g qui correspond à un taku de 9 pences (p) qui semble avoir existé chez les Fanti, et que l'on retrouve ultérieurement dans une liste recueillie par Garrard (page 341).
Garrard fait cependant ensuite état d'une information contradictoire qu'il a trouvée dans Horton (1868) qui donne à ce poids de 9 p, toujours en pays fanti, le nom de teycoo na simpoir. Simpoir (sempowa) valant 3 p, on retombe sur le taku de 6 p. Horton cite par ailleurs ce teycoo de 6 p, ainsi qu'un archi de 1 $, égal à 4 s 6 d. On ne saurait mieux décrire un T de 0,22 g et 1 A* de 1,95 g, ce qui là aussi réfère au système dualiste (Garrard, 1980).

1874. Bonnat ; 1875. Kuhne et Ramseyer, cité par Menzel :
Marie-Joseph Bonnat, négociant français, a été otage des Ashanti de 1869 à 1874. Ses notes, retrouvées tardivement, ont été publiées en 1994. Il y décrit longuement la société ashanti.
Les pasteurs suisses Kuehne et Ramseyer, ainsi que M^me Ramseyer ont partagé cette captivité et en ont fait un récit indépendant.
Bien que pourvu d'or et poids pour son quotidien par ses hôtes forcés, Bonnat n'en a pas détaillé le fonctionnement. Il nous apprend cependant au fil des pages que 6 tacous valent 4,80 F, (page 327), que 2 periguans valent 72 $, (page 405) et que 20 periguans pèsent 45 onces (de 32 g ³) (page 396). Bonnat nous explique aussi comment les Ashanti, ayant épuisé leurs ressources naturelles d'or en poudre, s'y prenaient pour en fabriquer à partir de pépites afin d'assurer leur circulation monétaire (Perrot, 1984).
Kuehne de son côté rapporte une liste détaillée des poids ashanti avec leur correspondance en dakoo et en dollars qui nous apprend que 1 dollar américain vaut 8 dakoo. Une once de poudre d'or payée 16 $ vaut 3 £ 12 à la côte et que pour les Fanti 1 $ vaut 1 ackie de poudre d'or et qu'un pereguin est compté pour 36 $ (Menzel 1968).
De ces informations on retient de Bonnat que le tacou vaut 80 c et pèse 1/3 g x 0,80 = 0,26 g et qu'un periguan pèse 2,25 onces, soit 72 g, ce qui correspond au poids que donne Zeller au pereguan lourd ⁴.
On retient de Kuehne que le dollar correspond 1,95 g d'or akan, que le dakoo pèse 0,243 g et que le pereguin pèse 70,2 g.
Bien que Bonnat attribue au taku une valeur trop élevée, ces données sont cohérentes avec le système de poids forts.

1875. Christaller :
Johann Christaller, missionnaire allemand vécu de 1853 à 1868 au Ghana. Il est un des premiers traducteur du Twi, la langue des Akan. Selon Zeller, il fait état d'un double système de poids et aussi de balances, différents pour acheter ou vendre (Zeller, 1913).

1889. Binger :
Entre 1887 et 1889, le capitaine Binger explore l'Afrique de l'ouest du Niger au golfe du Guinée. Il est le dernier auteur à témoigner d'un système monétaire akan en activité. Il nous renseigne sur les monnaies en cours à Salaga, à Bondoukou et en pays Agni. Binger compte en once de traite de 32 g, et évalue le gramme d'or akan à 3 f soit 0,33 g pour 1 franc ⁵.
À Salaga (au nord-est de Kumasi), on paye en cauris mais aussi en poids de métal : barifari de 17,6 g et mitqal de 4 g, bien que 1 barifari soit censé faire 4 mitqal.
À Bondoukou ⁶, on paye en cauris, mais aussi en graines et en poids métal. La plus petite graine, le damma, vaut 2,25 f et pèse donc 0,075 g ce qui correspond aux poids faibles.
Le barifari pèse 16 g et le mitqal 4 g. Il note aussi que les petits poids sont trop forts et que les marchands achètent aux prospecteurs l'or avec des poids forts, et le revendent aux Achanti avec des poids faibles.
En pays Agni au sud-est de la Côte d'Ivoire les cauris n'ont plus cours. Binger dresse une liste très complète des poids agni, avec leurs équivalents en francs. On en retient pour notre propos que l'once fait 16 aké à 6 f, que chaque aké vaut 12 ba (parfois appelés tacou) à 50 centimes et que le damma vaut 0,25 f. Le barifari pèse 16 g. Un damma pèse 0,082 g, et un taku 0,164 g ce qui correspond en fait au B*. On a donc un barifari qui varie de 17,6 g à 16 g, ce que Binger explique par l'imprécision et l'usure, et un damma qui varie de 0,075 g à 0,082 g ce qui là encore pose les bases d'un système dualiste.
À noter que 3 ba agni de Binger à 50 c valent à peu près 2 tacou ashanti de Bonnat à 80 c, dans le rapport habituel de 3 pour 2 entre ces deux unités (Binger, 1892).

Après 1900. Garrard et Abel :
Les informations d'Abel ont été recueillies en 1952 chez les Agni, les Baoulé et les Abouré. Aucun des notables interrogés, même les plus âgés, ne savait encore manier les poids, mais la plupart se souvenait de l'existence de poids mâles et femelles (Abel, 1973).
Garrard rapporte 12 listes provenant d'informateurs issus des différents états Akan. Le plus âgé est né en 1872. Les valeurs des poids sont données en monnaie anglaise. Elles sont calculées au cours de 3£ 12 s l'once, donc dans le système faible, avec un taku à 6 p, soit 0,22 g. Aucun d'entre eux ne se souvient de l'existence de poids mâles et femelles, pas plus qu'il ne cite jamais le nom du mitqal (Garrard, 1980).

Discussion

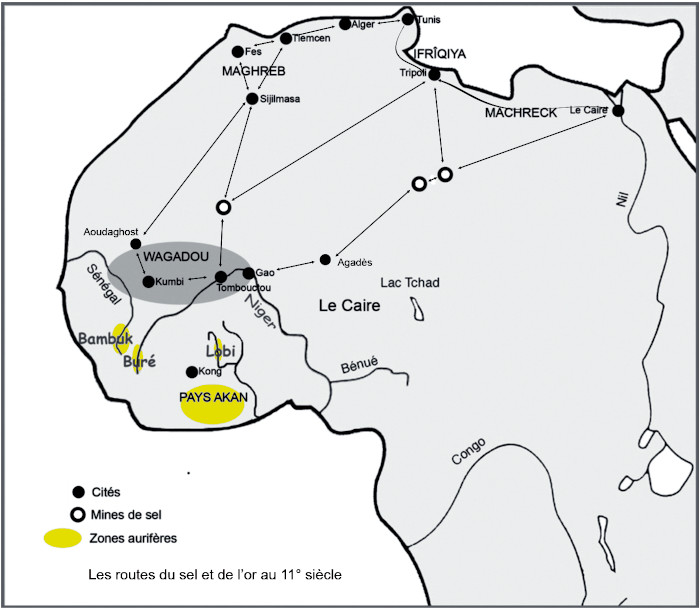
Sur douze témoignages recensés, seuls trois ne font aucun état des graines, ceux de Dapper et de Barbot, et celui de Bouët (qui cite cependant le takon) mais tous parlent de l'aké, comme du 1/16 d'once. Dapper, Barbot et Binger font directement état d'un système dualiste, qui transparaît par ailleurs à travers les incohérences des autres listes. Nous sommes en fait en présence de deux systèmes clos, qui ne communiquent que par des transactions commerciales. Le système akan d'un côté, le système européen de l'autre. Les Akan fonctionnent à prix constant et à poids variable, les Européens à poids constant et prix variable. Nous n'avons de renseignements sur le premier que par le truchement du second.

D'un côté, les transactions internes aux Akan qui se font par échange de poudre d'or. Peu leur importe sa teneur, ils ne sont pas à même de l'évaluer avec précision. Dès lors que la qualité de l'or est jugée acceptable par les deux parties, ne compte que la différence entre poids acheteurs et poids vendeurs. Pour le commerce de détail qui fait l'essentiel des ventes entre Akan, ils utilisent les petits poids ⁷. Pour le commerce de gros avec les européens, les marchands utilisent les plus fortes valeurs, benda ou au-delà, en utilisant ceux de leurs poids qui correspondent à leurs interlocuteurs.

De l'autre côté, les Européens. Nous choisirons les Anglais car ce sont ceux sur lesquels nous sommes le mieux documentés. Leur monnaie, la livre sterling (£), ou souverain d'or, est stabilisée depuis 1816 à 8 g d'or à 916 ‰ (22 carats) soit 7,32 g d'or fin. Leur objectif est d'acquérir de l'or contre des marchandises qu'ils ont réglées en £ à leurs fournisseurs. Ils calculent leur bénéfice dans cette monnaie, en tenant compte de la qualité de l'or qu'ils obtiennent en paiement. Ils pèsent l'or en once troy, avec leurs balances et leurs poids, mais ils ne peuvent pas imposer leurs pesées car leurs interlocuteurs sont capables de vérifier les transactions avec leur propre appareillage. C'est à cette occasion que les informations sur les systèmes pondéraux respectifs sont échangées. Chaque européen n'a donc à connaître que la partie du système akan qui correspond à ses poids.

Si on comprend aisément que les transactions se soient faites avec les Portugais dans le système faible (onça de 28,7 g), puis avec les Hollandais et les Anglais dans le système fort (once troy de 30,6 et 31,1 g), il reste à expliquer pourquoi, dans le dernier quart du 19^e siècle, on recourt de nouveau au système faible. Tout se passe comme si l'or akan avait été dévalué de 925 ‰ (22,2 carats) à 800 ‰ (19,2 carats), ce qui peut s'expliquer par la raréfaction de la poudre d'or naturelle dont la pureté dépasse les 22 carats et son remplacement par des pépites, de moindre teneur, ou de la poudre artificielle comme savaient la fabriquer les Ashanti. On a alors du mal à comprendre pourquoi les conversions se seraient faites dans le premier cas dans le système fort, et dans le second dans le système faible. L'inverse semble plus logique, l'acheteur akan devant donner plus d'or pour obtenir le même produit du marchand anglais. Pour comprendre analysons la vente d'un fusil de traite.

En 1820, le prix d'un fusil Brown Bess ⁸ est de l'ordre de 1 £. Une ozt d'or ayant un pouvoir d'achat de 4 £, il en faut 7,8 g pour 1 £. Pour l'acheteur akan il faut acquitter 4 A* à 1,95 g ou 32 T* à 0,24 g. La transaction se fait donc dans le système fort. En 1870, une ozt d'or n'a plus qu'un pouvoir d'achat de 3 £ 12 s, il en faut 8,8 g pour 1 £. Pour l'acheteur akan, cette somme correspond à 5 A de 1,76 g ou 40 T de 0,22 g. La transaction se fait alors pour lui dans le système faible. Le passage d'un système à l'autre s'est donc fait simplement, sans que le commerçant anglais n'en ait conscience et ne puisse donc en faire état.

Conclusion

Notre article princeps avait mis en évidence la dualité des poids, mais sans pouvoir affirmer, du fait de l'hétérogénéité dans le temps et l'espace de la collection sur laquelle notre étude portait, qu'il s'agissait bien d'un système intégré poids-acheteur/poids-vendeur. Cette analyse des sources conforte la vraisemblance de cette théorie dualiste, qui est au fond, plus que le poids du taku, le point essentiel du Système Pondéral Akan.

Histoire de mitqal

Que dire maintenant du mitqal dont Zeller affirme qu'il n'est pas utilisé en Gold-Coast, mais dont Garrard fait la pierre angulaire du système pondéral akan. Se pourrait-il que comme les poids correspondant aux poids européens, il ne soit qu'une des multiples facettes du système akan, utilisé dans le commerce avec l'Afrique du Nord ?

Résumons la thèse de Garrard

En l'an 600, les poids et les monnaies en usage dans les mondes méditerranéen et moyen-oriental sont ceux des Byzantins, hérités des Romains, et ceux des Perses, lointain héritage des Grecs d'Alexandre le Grand. Cinquante ans plus tard, après avoir conquis une grande partie de ces empires, les Arabes fusionnent ces monnaies perses et byzantines dans leur système bimétallique. Des premiers, ils adoptent la drachmé, pièce d'argent dont ils font leur dirhem, des seconds le denarius aureus, pièce d'or dont ils font leur dinar. Pour la pesée, ils conservent les unités de poids romaines en usage. L'uncia de 27,3 g prend le nom d'uqiya et la sextula, son sixième devient le mitqal ⁹, ce qui lui donne la masse de 4,55 g. Poids et monnaies se rejoignent au niveau du dinar et du mitqal, deux termes finiront par signifier la même chose. Ce système atteint le Sahel par le Sahara, puis les Akan, en même temps que le procédé de fabrication des poids. Les Akan auraient ainsi importé un système basé sur le mitqal avec pour preuve la découverte de poids très anciens, en terre cuite, à ce standard. Ils se seraient ensuite adaptés aux poids européens, au fur et à mesure de l'arrivée sur les côtes du golfe de Guinée des Portugais, des Hollandais et des Anglais ¹⁰. Garrard, après un exposé historique très documenté sur le dinar, mais finalement sans rapport avec sa conclusion, nous dit que ce serait cette uqiya de 27,3 g, ramenée, il ne dit pas pourquoi, à 26,4 g, divisible en 6 mitqal de 4,4 g et dite once de traite, qui aurait été utilisée au Soudan ¹¹ pour le commerce de l'or.

Discussion

Le problème est que nous n'avons pas retrouvé trace d'un dinar ni d'un mitqal de 4,40 g à quelle époque que ce soit dans un pays d'Afrique du Nord impliqué dans la traite transsaharienne. En Égypte, point de départ des caravanes de l'est, le dinar, vers 1200, pèse 4 g. Au Maroc, d'où viennent celles du nord, son poids nominal varie de 4,25 g vers 1050 à 4,72 g vers 1130 (voir encadré et carte).

Pour nous y retrouver, voyons de façon schématique le parcours d'une once d'or versus celui d'une charge de sel vers 1150, une date à laquelle les Akan sont vraisemblablement déjà intégrés dans la traite transsaharienne en tant que producteurs d'or :
- Au nord, les Berbères du Maroc, qui contrôlent les mines de sel du Sahara. Ils utilisent entre eux des dinars, dont ils peuvent contrôler la masse avec le mitqal correspondant, mais qui dans leur commerce avec le Soudan ne sont qu'une unité de compte dont les espèces ne circulent pas ¹². Ils comptent à cette époque en dinars almohade de 4,7 g. Ils utilisent des poids monétaires de verre ou de laiton pour peser l'or qu'ils échangent contre le sel. Leurs dinars font 23 carats.
- Au sud, les Akan, qui ont domestiqué la forêt et dont on ne sait pas grand-chose à cette époque. Nous supposerons qu'ils utilisent déjà comme monnaie la poudre d'or et qu'ils la pèsent avec des graines de damma ou de taku dans leur système dualiste. Ils ont de l'or d'une grand pureté, mais pas de sel.
- Entre eux, les Dioula. Cette caste de commerçants soninké islamisés monopolise le commerce le long du Niger, où aboutissent à Tombouctou les caravanes venues du nord. Ils échangent le sel contre de l'or, en poudre ou en pépites. Les transactions se font en mitqal. Ils apprennent auprès d'eux à les manipuler et à en fabriquer eux-mêmes à la cire perdue. Ils troquent ensuite le sel contre de l'or dans les zones de production, dont les plus proches sont le Bambuk au Sénégal, et le Buré en Guinée. Ce troc s'y fait parfois dit-on à la muette ¹³, en tout cas sans pesée, en fonction d'une offre et d'une demande qu'on peut penser régulées par des critères traditionnels. Ces gisements s'épuisant, les Dioula s'aventurent plus au sud, jusqu'à la lisière de la forêt où ils fondent, vers 1050 selon Binger, la ville de Kong au contact des Akan, avec qui l'or n'est pas simplement troqué à l'estime, mais pesé. De tous les producteurs d'or fréquentés par les Dioula, ils sont les seuls avec qui ce se soit passé ainsi. C'est logique si on admet qu'ils avaient déjà leur propre système de pesée dans lequel le mitqal s'est retrouvé en phase avec un poids akan.

S'il s'agit bien de nso-nsa, le nom qui nous est parvenu, c'est-à-dire 7x3, et si on conserve au taku sa valeur de 0,22 g dans le système faible, ce poids doit peser 0,22 x 21= 4,6 g ce qui correspond à un dinar almohade à quasi parité de titre ce qui est tout à fait vraisemblable car l'or des Akan était considéré comme très pur. D'où vient alors que nso-nsa soit donné dans toutes les listes de poids que nous avons étudié pour 20 taku, ce qui aurait dû se dire nun-nan (5x4) dans notre terminologie simplifiée.

7x3 = 20 ou la croisée des mondes
Nous sommes maintenant à la fin du 15^e siècle. Les échanges entre Akan et Dioula se font toujours sur la base d'un mitqal de 4,72 g, soit 21 taku dans le système faible. Ces mitqal se mesurent avec des poids monétaires de laiton dont les Akan maîtrisent la fabrication. Ils ont adopté pour leur commerce extérieur de cette unité, très largement utilisée dans le monde méditerranéen et bien connue des navigateurs portugais avec qui ils viennent de commencer à échanger.

Les Portugais utilisent comme unité de mesure pour les métaux précieux l'onça, en fait l'once de Cologne, de ≈ 28,7 g, qui se divise par 4, 8,16 et 32 mais aussi par 24 ce qui correspond à 1 escrupulos de ≈ 1,16 g (Doursther, 1840 ). Quatre de ces escrupulos pèsent ≈ 4,64 g soit presque exactement nso-nsa. Du fait de cette coïncidence, les Akan n'auraient rien eu à changer dans leurs habitudes pour contrôler les pesées des Portugais si ceux-ci avaient comme les Dioula utilisé des poids monétaires. Mais, parce que c'est plus facile en voyage, ils utilisaient des piles à godet dont chacun pèse la moitié du précédent (voir le détail du tableau de Quentin Metsys), avec lesquelles il n'est donc pas possible de peser 1/6 d'once, mais de l'approcher en additionnant deux godets de 1/8 et de 1/32 = 5/32 (≈ 4,5 g).

Si on admet que cette traite se soit faite en mitqal, unité connue des deux parties, les Akan pour s'adapter sont passés de leurs multiples par 3, 6, 12… à ceux par 2, 4, 8... et donc de nso-nsa à nun-nan. La différence était faible et de leur point de vue, ils y gagnaient au change. Quant aux Portugais, l'or des Akan était pour eux une telle aubaine que même s'ils avaient eu conscience de cette subtilité, ils n'en auraient eu cure.

Quand, pourquoi et comment la confusion des noms s'est-elle produite entre le poids utilisé avec les Dioula et son succédané avec les Portugais ? On ne saura jamais, mais on comprend qu'à force de mélanges, de recombinaisons et d'approximations, ce glissement sémantique se soit produit au fil des siècles. Cette incongruité mathématique serait ainsi la trace de l'entrée des Akan dans la première mondialisation, la croisée des mondes européen et africains.

Conclusion

Tout se passe bien comme si la diversité de leurs poids avait permis aux Akan de s'adapter au système arabe de la même façon qu'ils s'adapteraient plus tard aux systèmes européens. Le mitqal n'en serait qu'un invité, pas le socle. Au fur et à mesure que nous progressons dans notre enquête, l'image d'un système pondéral akan autonome et autochtone se fait de plus en plus nette. Il est difficile cependant de penser qu'il ait pu naître au sein de la forêt pour la simple raison qu'on n'y trouvait pas les métaux propres à la fabrication des balances sans lesquels les pesées, même en graines, n'auraient pu se faire. Les Akan se disent les descendants de l'empire du Wagadou ¹⁴, légende dont on ne connaît pas la part de vérité. Les balances, les poids y étaient connus pour le commerce de l'or, qui se faisait déjà avec l'Afrique du Nord, et l'Abrus precatorius, dont les graines rouges et noires font le damma, ainsi que le Parkia biglobosa, dont les graines noires sont peut-être le taku, y poussaient. L'interpénétration entre système métallique arabe et système grainier africain a donc pu se faire à cet endroit, avant que les Akan n'émigrent vers le sud, vers la forêt, pour échapper à l'islamisation imposée par les Almoravides.

Références bibliographiques

Ben Rhombdane K., 1979. Supplément au catalogue des monnaies musulmanes de la Bibliothèque nationale : monnaies almoravides et almohades. Revue Numismatique, 21 : 141-175.

Binger L. G., 1892. Du Niger au Golfe de Guinée par le pays de Kong et le Mossi. Paris, Hachette, 2 vol. (vol. premier, 513 p. ; vol. second, 414 p.).

Bosman W., 1705. A new and accurate description of the coast of Guinea, divided into the Gold, the Slave, and the Ivory coasts. London, Ballantyne Press, 512 p. [Ed. Frank Cass, 1967].

Bouët-Willaumez L.-E., 1848. Commerce et traite des noirs aux côtes occidentales d'Afrique. Paris, Imprimerie Nationale, 230 p.

Bowdich T. E., 1819. Mission from Cape Coast Castle to Ashantee, with a statistical account of that kingdom, and geographical notices of other parts of the Interior of Africa. London, John Murray, 512 p. [Ed. Frank Cass, 1966].

Dapper O., 2007 [1686]. Description de l'Afrique, contenant Les Noms, la Situation & les Confins de toutes ses Parties, leurs Rivières, leurs Villes & leurs Habitations, leurs Plantes & leurs Animaux ; les Mœurs, les Coûtumes, la Langue, les Richesses, la Religion & le Gouvernement de ses Peuples. Avec Des Cartes des Etats, des Provinces & des Villes, & des Figures en Taille-douce, qui représentent les habits & les principales Ceremonies des Habitans, les Plantes & les Animaux les moins connus. Amsterdam, chez Wolfgang, Waesberge, Boom & van Someren, 534 p., 42 pl. http://catalogue.bnf.fr/ark:/12148/cb34554868. Consulté en ligne en septembre 2017.

De Marees P., 1605. Description et récit historial du riche royaume d'or de Gunea (sic), aultrement nommé, la coste d'or de Mina, gisante en certain endroict d'Africque. Amsterdam, chez Cornille Claesson, 100 p. [Les éditions Chapitre.com, 2017]

Debien G., Delafosse M. & Thilmans G., 1979, Journal d'un voyage de traite en Guinée, à Cayenne et aux Antilles fait par Jean Barbot en 1678-1679. Bulletin de l'Institut fondamental d'Afrique noire (série B), 40 (2) : 235-395.

Doursther H., 1840. Dictionnaire universel des poids et mesures anciens et modernes. Bruxelles, Hayez, 603 p.

Garrard T. F., 1980. Akan weights and the gold trade. Legon history series. London, Longman, 393 p.

Guilhiermoz P., 1906. Note sur les poids du moyen âge (première partie). Bibliothèque de l'école des chartes, 67 : 161-233.

Menzel B., 1968. Goldgewichte aus Ghana. Berlin, Museum für völkerkunde, Neue Folge, 12, Abteilung Afrika III, 241 p.

Müller W. J.,1676. Die Afrikanische auf der guineischen Gold-Cust gelegene Landschaft Fetu. Hamburg, Zacharias Härtel (3^e ed.)

Perrot C.-H., van Dantzig A., 1994. Marie-Joseph Bonnat et les Ashanti-Journal (1869-1874). Coll. Mémoires de la Société des Africanistes. Paris, Société des Africanistes, 672 p.

Roux C. & Guerra M.F, 2000. La monnaie Almoravide : de l'Afrique à l'Espagne. ArchéoSciences, revue d'archéométrie, 24 : 39-52.

Zeller R., 1913. Die goldgewichte von Asante (westafrika) eine ethnologische Studie. Leipzig, Teubner, 77 p.

Annexe

1. Traduction de l'auteur. ⇧
   

2. Ce qui correspond à un titre d'or fin de 925‰, supérieur à celui de la pièce d'or d'un souverain qui est de 916 ‰. ⇧
   

3. Bonnat compte vraisemblablement en once de traite de 32 g, unité utilisée dans les comptoirs français en Afrique. Ses biographes semblent s'être trompés sur ce point de détail. ⇧
   

4. Pour Zeller, le pereguan vaut 288 T* et pèse donc 72 g. Voir La table de multiplication akan, tableau 2. ⇧
   

5. 1 franc or pèse 0,32 g à 900‰, soit 0,29 g d'or fin. Le titre de l'or akan est donc estimé à 878 ‰. ⇧
   

6. À la frontière entre Côte d'Ivoire et Ghana, à l'est du pays baoulé. ⇧
   

7. À noter qu'un seul système de poids suffit aux achats directs auprès des producteurs, puis qu'il n'y a pas d'intermédiaire qui ait son bénéfice à prendre. ⇧
   

8. Le Brown Bess, ou long pattern rifle, le fusil des fantassins anglais pendant les guerres napoléoniennes, était très prisé pour sa robustesse par les Africains. La plupart des informateurs font état d'un prix entre 3 et 4 A*. ⇧
   

9. Mitqal, en arabe, aurait le sens de masse (Doursther, 1840). ⇧
   

10. On relève plusieurs inexactitudes dans le livre de Garrard. Premièrement, ce ne sont pas les Arabes qui ont « inventé » le dinar, mais les Perses, à la suite semble-t-il d'une confusion de poids et de terme entre denarius d'argent d'un poids de 4,5 g et l'aureus, appelé improprement denarius aureus. Deuxièmement, le poids de l'aureus de Dioclétien auquel il donne la valeur de 4,7 g beaucoup flotté, variant de ≈ 5,6 à ≈ 4,8 g, mais étant le plus souvent > 5,45 g. Enfin, le dinar almohade du 12^e siècle ne pesait pas 4,5 g, mais 4,72 g. Ces détails influent peu sur sa thèse puisqu'en définitive, il ne tient compte que de l'once romaine de 27 g et de son 1/6. ⇧
    

11. En arabe soudan signifie littéralement pays des Noirs, par opposition à beidan, pays des Blancs (l'Afrique du Nord). ⇧
    

12. Il serait absurde d'acheter de la poudre d'or avec des pièces en or. ⇧
    

13. Pour assurer leur sécurité, les deux parties ne se rencontrent pas. Les dioula déposent leur sel, les producteurs déposent une certaine quantité d'or en échange, et ainsi de suite jusqu'à tomber d'accord. ⇧
    

14. Empire médiéval africain mieux connu sous le nom d'Empire du Ghana. ⇧
    

Jean-Jacques Crappier
Collectionneur, Le Mans, France
Email : Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.