Vol. 3/1 | 2020 | Crappier & Gascou (fr)

En complément d'une précédente communication qui a montré la sophistication et l'origine africaine du système pondéral akan, cet article explique comment, par la compilation de travaux antérieurs vieux parfois de plus d'un siècle, les auteurs ont compris qu'il s'agissait d'un système dualiste poids-faible/poids-forts et reconstitué la table de multiplication qui sous-tendait la valeur de ses différentes unités. Ces hypothèses ayant été démontrées avec un très fort niveau de preuve par l'étude de milliers de poids, il reste à comprendre comment les Akan ont pu procéder à des multiplications aussi complexes que, par exemple 13 par 192, sans pouvoir, faute de numération écrite, poser l'opération.

Mots clés : akan - ashanti - baoulé - poids à peser l'or - Ghana - Côte d'Ivoire - Gold Coast - système dualiste - ethno-mathématiques - Timothy Garrard - Henry Abel - Rudolph Zeller - Louis Binger - taku - ba - mitqal - proto-monnaie

In addition to a previous communication which showed the sophistication and the African origin of the Akan Weighing System, this article explains how, by the compilation of previous works sometimes more than a century old, the authors understood that it's acted of a dualistic system light weight / heavy weight and reconstituted the multiplication table which underlined the value of its various units. These hypotheses having been demonstrated with a very high level of evidence by the study of thousands of weights, it remains to understand how the Akan were able to carry out multiplications as complex as, for example 13 by 192, without power, for lack of counting written, ask the operation.

Keywords: akan - ashanti - baule - gold weight (goldweight, goldgewitch) - Ghana - Côte d'Ivoire - Gold Coast - dualistic system - ethnomathematics - Timothy Garrard - Henry Abel - Rudolph Zeller - Louis Binger - taku - ba - mitqal - proto-currency

Introduction

Cet article est le deuxième d'une série consacrée à l'étude des poids à peser l'or des Akan, bien connus des collectionneurs et des ethnologues, mais dont le fonctionnement a suscité peu de recherches et reste mal connu. Dans notre article princeps (Crappier et al., 2019), nous avons montré, par l'étude de la plus grande collection de poids géométriques jamais étudiée (9031 dont 298 poids de chef de plus de 80 g), l'organisation et la précision de ce système pondéral et invalidé la théorie qui le faisait dériver de celui des Arabes, au profit d'une origine africaine.

Notre raisonnement suppose que la distribution des poids ait obéit à une table de multiplication complexe, que nous n'avions que brièvement expliquée, afin de ne pas alourdir notre démonstration. Notre propos est de combler ici cette lacune et de montrer comment cette table de multiplication dite akan a été construite et de réfléchir aux problèmes qu'elle soulève.

Méthode

Pour pénétrer le système pondéral akan, nous disposons des listes de poids dressées à partir du début du 17^e siècle par des marchands ou des explorateurs européens et des enquêtes de terrain réalisées par Henri Abel et Timothy Garrard dans la 2^e moitié du 20^e siècle. Mais ces listes, établies dans des unités portugaises, hollandaises, anglaises ou françaises, sont plus ou moins exactes et complètes, et les enquêtes souffrent d'avoir été effectuées plusieurs générations après que l'usage des poids ne fut tombé en désuétude. L'interprétation des données se complique d'une grande variabilité linguistique et d'un enchevêtrement progressif au fil du temps. Il n'est donc pas étonnant que les auteurs qui ont étudié ce système au cours du 20^e siècle soient tous arrivés à des conclusions différentes sur la nature et le fonctionnement du système pondéral akan, et que les travaux en soient restés là.

Malgré le recul du temps et l'incertitude sur les données, il nous a paru possible de proposer une synthèse des différentes théories à partir de quatre sources qui sont dans l'ordre chronologique les publications de Louis Gustave Binger en 1892, de Rudolph Zeller en 1903, de Henri Abel de 1952 à 1973 et de Timothy Garrard en 1982. Nous avons décortiqué les listes de poids rapportées par ces auteurs pour en comprendre la structure. Nous les restituons sous forme de tableaux qu'un survol suffit pour comprendre le raisonnement qui nous a conduit à la table de multiplication akan. Le lecteur intéressé trouvera des informations plus détaillées dans les encadrés.

Résultats

Les listes de poids permettent de se faire une idée précise du rapport entre elles des principales dénominations akan, mais établies pour la plupart en contre-valeur monétaires, elles ne nous en donnent pas directement la masse. Pour la calculer, il faut donc connaître le prix auquel se négociait une once d'or akan, sachant que ces onces, comme les monnaies, différaient d'un pays à l'autre, que la teneur en métal fin était diversement appréciée par les Européens et qu'elle variait selon qu'il s'agissait de poudre d'or ou de pépites.

Trois sortes d'unités se distinguent :

- des unités de base qui reposent sur des graines, le ba, et le taku, dans un rapport entre elles de 3 ba pour 2 taku ¹. Le ba vaut 2 damma, c'est-à-dire deux graines d'Abrus precatorius, une liane forestière. Le taku est aussi une graine, mais sa nature exacte est inconnue ;

- l'aké ² est une autre unité fréquemment citée, donnée pour 1/16 d'once. Un aké vaut 8 taku ;

- le benna ³ qui vaut 2 onces, qu'elles soient portugaises, hollandaises, anglaises, vaut donc 256 taku.

De façon générale le nom akan des poids est formé d'un radical (ba ou taku pour les petites unités) suivi d'un suffixe qui peut signifier soit une « multiplication par », soit plus rarement une « addition de ». On dénombre ainsi une vingtaine de radicaux et leurs multiples par 1/2, 2, 3 ou 4, jusqu'à 8 parfois, correspondant à une soixantaine de poids différents.

Numération normalisée

Bien qu'elles appartiennent au même groupe linguistique, les langues akan diffèrent notablement d'un état à l'autre et les appellations des poids varient, en particulier entre états de l'est et de l'ouest (voir carte et Annexe 1), ou prennent des valeurs différentes. Pour faciliter la comparaison entre les différentes sources, nous avons simplifié et uniformisé la numération akan (Tableau 1). Le lecteur curieux se reportera à l'Annexe 2, reproduite de Bowdich, qui en montre toute la complexité (Bowdich, 1819). Dans le même esprit, nous avons utilisé des noms ashanti pour les listes est-Akan et des noms baoulé pour les listes ouest-Akan, avec leur orthographe la plus simple puisque la traduction européenne en est arbitraire. Enfin, pour éviter les confusions, le mot poids sera dorénavant réservé à la désignation des objets, et le mot masse à leur valeur en grammes.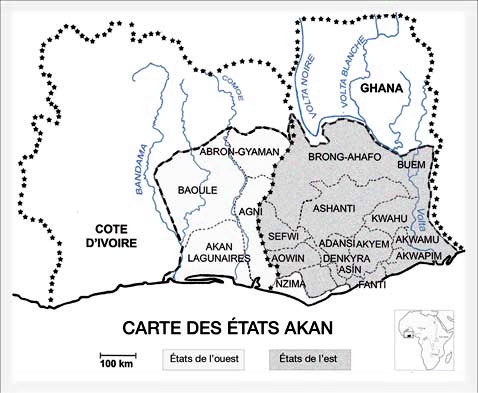

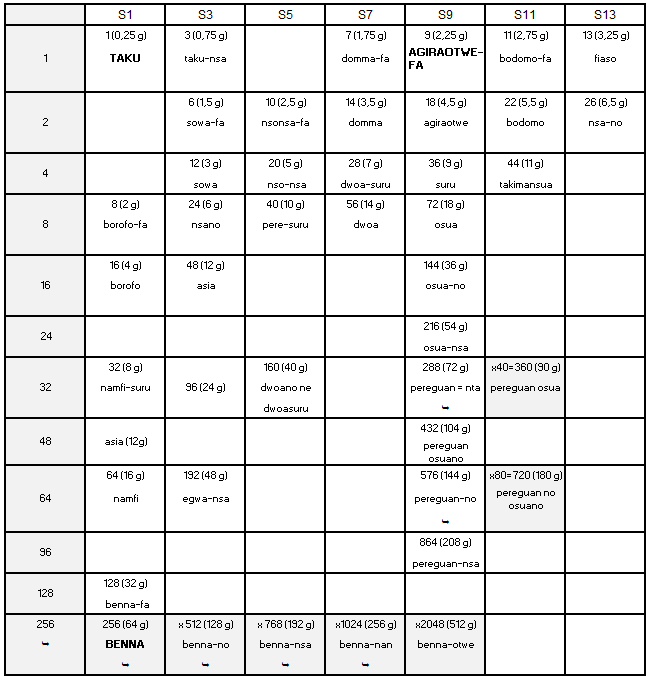
Tableau 1. Numération akan simplifiée.

Nomenclature des poids selon Zeller (1869-1940)

Rudolph Zeller, directeur de la section ethnographique du Musée historique de Berne est le premier, en 1913, à publier une synthèse du système pondéral akan à partir d'informations fournies par Rudolph Bürki, un missionnaire ayant vécu en Gold-Coast ⁴ au début du 20^e siècle et de listes plus anciennes, établies du temps où les poids étaient encore en usage. Les données sont d'origine akyem et ashanti, donc est-akan. Le système de Zeller repose sur le taku auquel il attribue le poids de 0,25 g. Il ne parle pas du ba. Il répartit les poids en 8 séries ⁵, dont les 7 principales ont pour premier terme 1, 3, 5, 7, 9, 11 et 13 taku et dont chaque élément est le double du précédent. Il présente ses résultats sous forme de tableau (Annexe 3) qu'on transforme facilement en une table de multiplication composée de 7 colonnes, une par série, dont les premiers poids sont respectivement 1, 3, 5, 7, 9, 11 et 13 taku, et d'une douzaine de lignes correspondant aux multiplicateurs par les puissances de 2, c'est-à-dire 2, 4, 8 etc. jusqu'à 2048 pour la série 1 (Tableau 2).

Tableau 2. 1 taku = 0,25 g. Appellations ashanti. Ce tableau a été établi à partir des tabelle III et IV de Zeller. Les valeurs sont données en taku.

Zeller affirme par ailleurs que le mitqal ⁶, le poids d'origine Arabe qui représente la masse d'un dinar ⁷, n'est pas utilisé en Gold-Coast et rapporte le témoignage de Christaller affirmant que les Akan utilisaient des poids différents pour acheter ou vendre (Zeller, 1903).

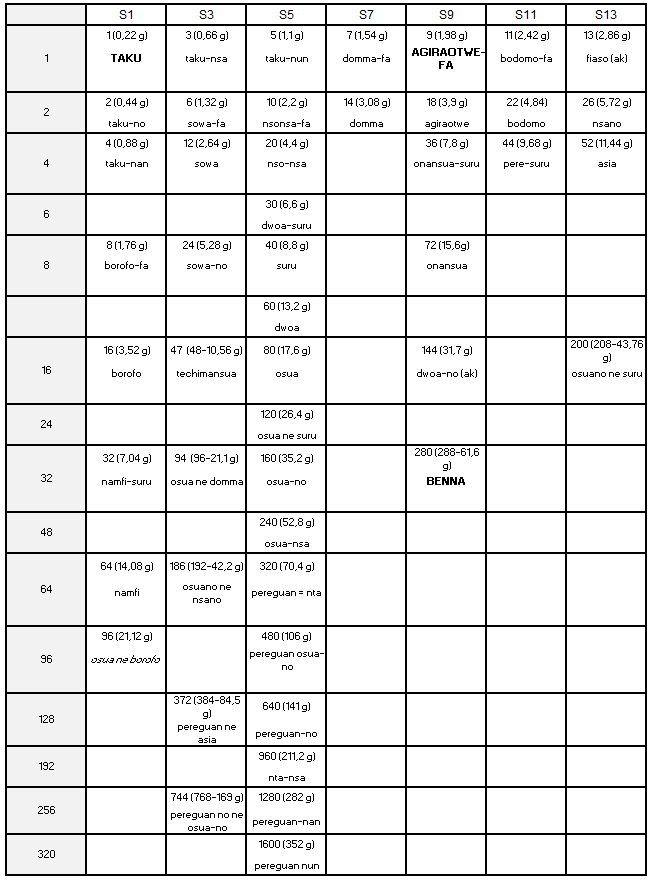
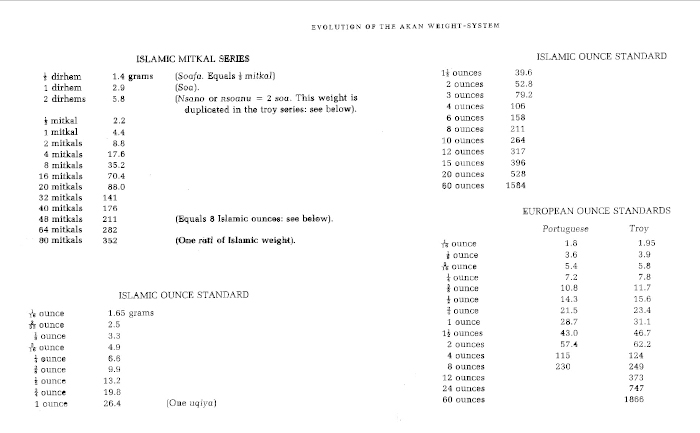
Nomenclature des poids selon Garrard (1943-2007)

Anglais d'origine, Timothy Garrard fit l'essentiel de sa carrière au Ghana comme juriste et comme ethnologue. Ses travaux font autorité en matière de poids. Sa théorie contredit celle de Zeller. Pour lui, il s'agit d'un emprunt aux Arabes dont l'unité de base était le mitqal de 4,4 g et l'uqiya, l'once arabe, de 26,4 g. Les Akan l'auraient appris des Dioula, caste de marchands Soninké islamisés, qui commerçaient avec les deux parties dans le cadre de la traite transsaharienne. Ils y auraient ensuite ajouté des poids européens, une fois le contact établi avec ces derniers, expliquant ainsi la complexité du système, composé selon lui de 4 séries, deux calquées sur les poids arabes (sur le mitqal et sur l'uqiya), une sur les poids portugais, et la dernière sur les poids anglais, chaque poids étant, dans chaque série, le double du précédent (Annexe 4). La série uquiya aurait été utilisée surtout chez les Akan de l'ouest.

Le taku, auquel il attribue la masse de 0,25 g comme Zeller, et le ba, n'y auraient tenu qu'un rôle accessoire pour les menues transactions. Il ne trouve pas trace dans ses enquêtes de différence entre poids pour vendre et poids pour acheter (Garrard, 1982).

Cette thèse est solidement étayée, mais se trouve contredite par les listes de poids qu'il a lui-même recueillies dans les différents états akan auprès de notables qui en connaissaient encore les noms et les contre-valeurs en monnaie anglaise. Aucun d'entre eux n'y cite le mitqal, mais tous font état d'un taku de 6 pences pesant 0,22 g. Le tableau de synthèse qu'il établit à partir des listes de 16 états différents est trop grand pour qu'on puisse le reporter ici. Nous n'en citons (Annexe 5) que les listes Ashanti et Akyem qui permettent de retrouver, sur la base d'un taku de 0,22 g, les 7 séries de Zeller, et de reconstituer, quoique dans un ordre différent, une table de multiplication (Tableau 3).

Tableau 3. 1 taku = 0,22 g. Appellations ashanti. D'après Garrard, p. 348-349. Les valeurs sont données en taku.

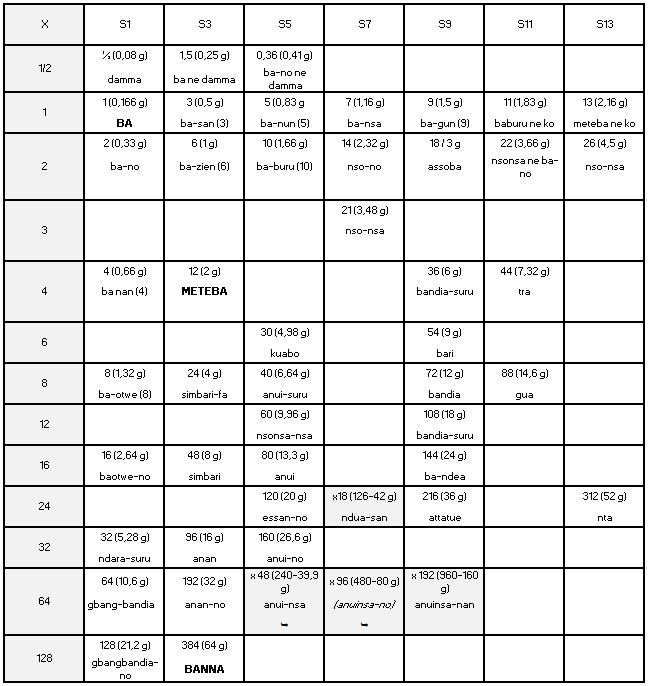
Nomenclature des poids selon Binger (1856-1936)

Capitaine d'Infanterie de Marine, Louis-Gustave Binger explora l'Afrique de l'ouest. Il finit sa carrière comme gouverneur de la Côte d'Ivoire. Le compte rendu de son voyage du Niger au Golfe de Guinée est notre troisième source (Binger, 1892). Précisément celui de son séjour en 1889 chez les Agni, des Akan de l'ouest, dont il consigna par écrit la liste des poids (Annexe 6). Elle est établie sur la base d'une once arrondie à 32 g et d'un cours de 3 francs or le gramme d'or. L'unité de base est le ba qui vaut 50 c et pèse donc 1,66 g. Il équivaut à 2/3 du taku de 0,25 g. La masse de la graine de damma est donc 0,83 g. Cette liste se prête comme les autres à la présentation en table de multiplication (Tableau 4), sur le modèle de celle du tableau 2.

Tableau 4. 1 ba = 0,166 g = 50 c. Appellations baoulé. D'après Binger. Les valeurs sont données en ba.

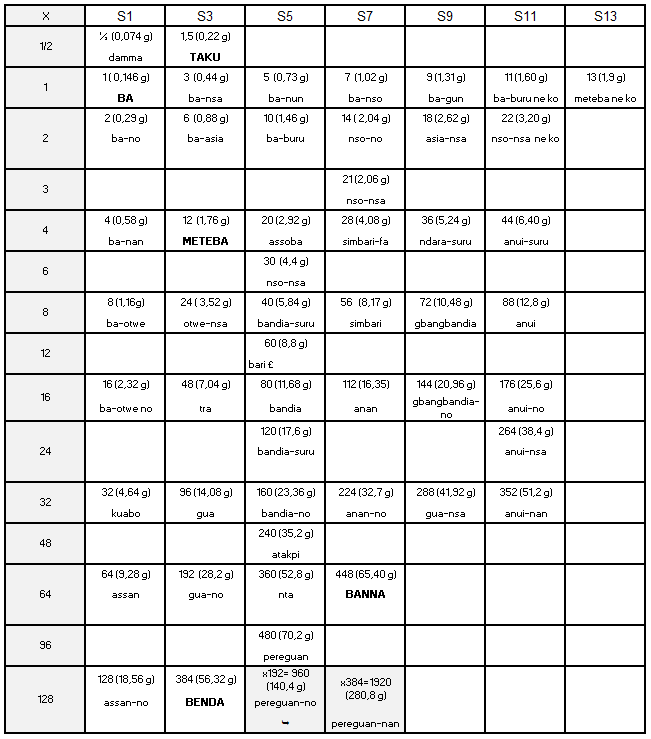
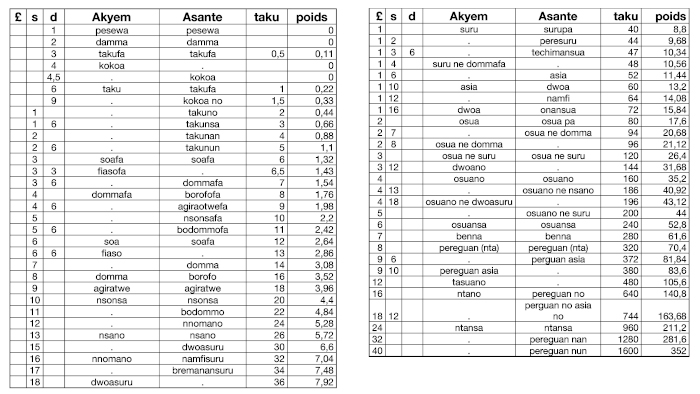
Nomenclature des poids selon Abel (1896-1958)

Administrateur colonial français, Henri Abel fut maire d'Abidjan de 1948 à 1952. Ses enquêtes de terrain en 1952 en pays Baoulé, Agni et Abouré, donc en zone ouest-akan, lui permirent de rencontrer des notables qui possédaient encore des poids, qu'ils ne savaient plus utiliser, mais dont ils connaissaient les noms et les contre-valeurs en Fr ou en £. Ses informateurs lui rapportent un système fondé sur le taku et sur le ba et comportant pour chaque unité des poids mâles et des poids femelles (Abel, 1973). L'analyse de leurs appellations lui permet de les classer en 7 séries comme Zeller et en les pesant, de calculer la masse du ba et du taku, respectivement 0,146 g et 0,22 g (dans le rapport de 3 pour 2). L'idée de transformer les listes en table de multiplication est de lui, mais celle qu'il établit, à la fois en ba et en taku, est complexe et bancale (Annexe 7). Reconstruite avec comme ligne de base 1, 3, 5, 7, 9, 11, 13 ba, elle retrouve une structure cohérente selon le modèle de Binger (Tableau 5).

Tableau 5. 1 ba = 0,146 g. 1 taku = 0,22 g. Appellations baoulé. D'après Abel. Les valeurs sont données en ba.

Synthèse

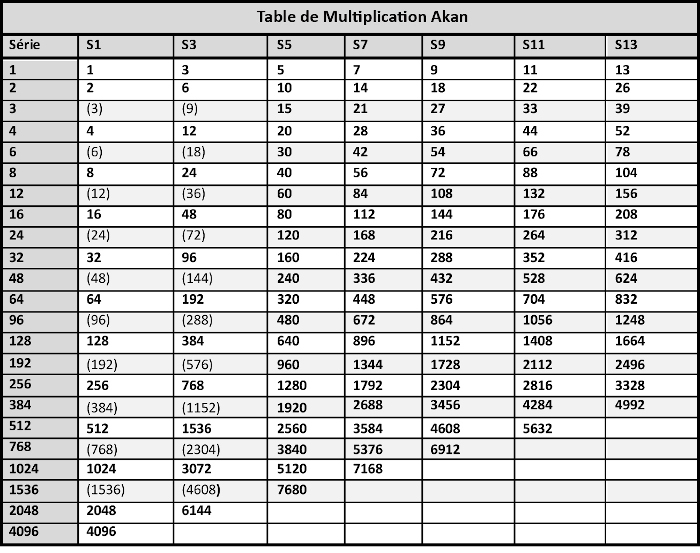
Quatre sources documentées et crédibles, des unités différentes, des interprétations contradictoires, mais quatre tableaux desquels se dégagent des enseignements sur le système pondéral des Akan :

- la possibilité de répartir les poids en 7 séries, au sein desquelles chaque unité est le multiple par 2, parfois par 3, de la précédente ;

- l'utilisation préférentielle du ba à l'ouest et du taku à l'est ;

- la coexistence d'unités légères et d'unités lourdes : à l'ouest un ba léger de 0,146 g et un ba lourd de 0,166 g, à l'est un taku léger de 0,22 g et un taku lourd de 0,25 g, dans un rapport léger/lourd de 8 pour 7 ;

- des appellations différentes entre l'ouest et l'est, mais qui au sein de chaque région sont communes aux poids faibles et forts. Parfois à valeur constante (les poids de même nom ont un nombre identique de graines mais une masse différente), parfois à masse constante (la masse est constante mais le nombre de graines est différent).

Nous en concluons que les Akan, dont les paiement de tous les jours se faisaient en poudre d'or, ont vraisemblablement utilisé, comme le disait Abel qui se trompait cependant sur sa nature ⁸, un système dualiste poids-faibles/poids-forts reposant sur la différence entre poids légers et lourds : ba et taku légers (notés maintenant B et T) pour acheter à prix faible, ou consentir un prêt, et ba et taku lourds (notés B* et T*) pour revendre à prix fort ou récupérer une créance avec intérêt.

Nous en déduisons aussi une table de multiplication commune aux deux régions et aux sous-systèmes faible et fort en compilant les tableaux 2, 3, 4 et 5, en complétant les cases manquantes et en ajoutant des multiplicateurs par 192, 384… 1536 que nous appelons table de multiplication akan (Annexe 7). Ce faisant, nous prévoyons des valeurs inconnues de nos sources mais que l'on devrait retrouver par la pesée des poids que nous avons colligés, en particuliers celle des 298 poids de chef.

Discussion

Même si nous avons pu montrer dans notre article princeps, avec un très fort niveau de preuve, la vraisemblance de nos conclusions, la table de multiplication akan n'en soulève pas moins de nombreuses questions théoriques et pratiques :

1. La précision au milligramme a-t-elle un sens ?

Il est évident qu'une telle précision était inaccessible aux Akan, étant donné la rusticité de leurs balances, mais rappelons qu'il s'agit de valeurs calculées et non pas de valeurs réelles. Ceci d'ailleurs ne les empêchait pas d'utiliser une unité encore plus légère que le ba, le pesewa, correspondant à un grain de riz, d'une masse de 0,04 g.

Cette précision dans les calculs est cependant nécessaire car si les arrondis dans la valeur du ba et du taku n'ont que peu de conséquences pour les petites et jusqu'aux moyennes valeurs, ils entraînent à partir de benna une dérive importante, dérive que l'on ne retrouve pas lors de la pesée des poids de chef et qui n'existait donc pas dans la réalité. Ce qui se comprend puisque plus le nombre de graines est grand, plus on se rapproche de leur valeur moyenne et donc plus la mesure peut être précise.

2. Que sait-on des unités de base ?

- Quelle est la nature du ba et du taku ?

Si le ba est bien identifié par la graine d'Abrus precatorius, le doute existe sur son poids exact. La graine qui correspond au taku n'est pas contre pas connue. Nous y revenons en détail dans un article dédié ⁹.

- Que sait-on de l'aké ?

Valant 1/16 d'once, il n'apparaît pas sous ce nom dans les listes de poids que nous avons étudiées. Il correspond au poids que les Akan appelaient métaba à l'ouest, agiraotwe-fa à l'est. L'origine du mot est sujette à controverse ¹⁰. En ce qui nous concerne, nous pensons qu'il s'agit du mot aquiay, qui en Brong Ahafo (alias Booroom, voir carte et Annexe 1), correspondait au nombre 8 et qui se dit dans les autres dialectes otwe, ou awotwe, ou encore oque dans la relation que fait de Marees de la côte de l'Or (de Marees, 1605). Aké signifierait donc simplement 8 taku.

Nous avons donc affaire à un aké léger de 1,79 g (noté A) et à un aké lourd de 1,94 g (noté A*).

- Quid du benda ?

Benna à l'est, banna ou benda à l'ouest, tous les auteurs lui donnent la valeur de 2 onces et le poids de 62 g dans l'un ou l'autre système faible ou fort. Abel est le seul à distinguer entre benda de 56 g et benna de 65 g. Nous en rediscuterons. Cette unité n'est pas rattachée à une graine.

3. Quels renseignements pouvons-nous tirer de ces tableaux ?

Ba et taku ont-ils une origine différente ?

Si on admet que la présentation en table de multiplication ait eu un sens réel pour les Akan, le fait qu'elles soient en taku à l'est, et en ba à l'ouest est un argument en faveur d'une séparation géographique des deux systèmes, bien que taku et aké aient aussi été en usage à l'ouest. Les tableaux ne nous apprennent rien par contre sur l'antériorité d'un système par rapport à l'autre.

Lequel des systèmes fort ou faible aurait-il précédé l'autre ?

Il y a plusieurs indices dans ces listes qui permettent d'en discuter. Ainsi, la régularité quasi parfaite des tableaux en T* comparée au désordre apparent des tableaux en T plaide pour une antériorité des premiers par rapport aux seconds. C'est ignorer qu'une des premières relations des poids akan, par de Marees, qui date de 1605, fait état d'un aké de 1,79 g et d'un benda de 57 g, appartenant à la série légère et que nso-nsa, qui correspond au mitqal et donc à la traite transsaharienne, encore plus ancienne, relève aussi de ce système. Il faut donc envisager une coexistence et une interpénétration des deux systèmes.

Peut-on en conclure que les deux systèmes aient cohabité ?

De même que le ba prédominait à l'ouest, et le taku à l'est, on peut penser que les différences entre poids faibles et poids forts correspondaient à des particularismes régionaux. Pour Ott, c'était le cas entre les états côtiers et ceux de l'intérieur. Il y voyait la façon dont les importateurs africains, qui se rendaient dans les forts de la côte pour acheter aux Européens les denrées qu'ils redistribuaient dans les terres, prenaient leur bénéfice (Ott, 1968).

Mais peser de l'or en poudre avec les balances, les cuillers et les conteneurs dont disposaient les Akan est malaisé, et rajouter un poids en cours de pesée fait prendre le risque de compromettre un équilibre précaire et de perdre de l'or. On peut donc poser l'hypothèse, avec Abel, d'un système dualiste utilisé au quotidien au sein de chaque état.

Pour imaginer comment cela aurait pu fonctionner, il faut distinguer deux cas de figure.

Les transactions directes entre producteur et consommateur dans lesquelles n'intervient que le prix que demande le vendeur, correspondant à une quantité d'or généralement fixée par la coutume et indiquée par le nom d'un poids. La négociation porte sur la qualité et la pesée de l'or, chacun utilisant ses propres poids pour vérifier la transaction. Un seul système de poids est nécessaire dans ce cas.

Dans le cas d'un prêt par contre, ou d'une revente par un marchand, le système dualiste prend tout son sens, le commerçant, ou le prêteur utilisant les poids-faibles pour acheter la marchandise, ou consentir le prêt, et les poids-forts pour la revendre ou récupérer la créance. La différence de poudre d'or entre poids vendeur et poids représentant leur bénéfice.

Deux questions se posent alors :

- La marge bénéficiaire de 1/7 (14%) est-elle cohérente avec cette hypothèse ? Ce taux paraît convenable pour un prêt, et même usuraire dans une économie sans inflation. Pour une vente par contre, le bénéfice paraît bien faible sauf si on tient compte du fait qu'il s'agissait d'un monde ne connaissant ni TVA, ni charges sociales et où les frais structurels étaient minimes. 14% de bénéfice net en fin d'exercice satisferait plus d'un commerçant de nos jours. Par ailleurs, en ce qui concerne le commerce avec les Arabes ou les Européens, la demande intérieure était telle que les intermédiaires, qu'ils soient Dioula ou Akan avaient vraisemblablement trouvé un moyen de prendre un bénéfice plus grand, soit en réduisant davantage les quantités, soit en augmentant quand même les prix.

- Comment expliquer que les informateurs européens n'aient pas signalé ce dualisme ?

Trois d'entre eux seulement y font référence de façon plus ou moins explicite, mais la plupart n'en parle pas. Nous y reviendrons dans le prochain article ¹¹. Ce système étant conçu pour les transactions entre Akan, il n'y avait pas de raison que les étrangers, qui se faisaient payer en poudre d'or des marchandises dont ils fixaient le prix en fonction de l'offre et de la demande, en aient été informés. La diversité des poids akan était telle qu'ils n'avaient à connaître du système que la partie qui correspondait à leur propres poids monétaires : faible pour le mitqal, l'uqiya et l'onça, fort pour les Ozt hollandaises et anglaises.

4. Une table de multiplication akan bien compliquée ! (Annexe 7)

- Nous n'avons que 10 doigts pour compter. Les séries 11 et 13 paraissent donc contre-intuitives. Existent-elles vraiment ?

- Pourquoi toutes ces cases supplémentaires par rapport à nos sources ? Existerait-il des unités manquantes, utilisées entre eux par les Akan mais inconnues de leurs partenaires européens ?

- La prédominance des multiples par 2 dans ces tableaux relève-t-elle d'un biais d'observation, lié à l'utilisation par les marchands européens de piles de poids qui sont conçues sur ce principe ¹².

L'étude de nos 298 poids de plus de 80 g, dits poids de chef, permet de répondre par l'affirmative à ces trois questions :

- Le tableau 6 montre les cases dans lesquels ils se répartissent selon la valeur dont ils sont le plus proche après transformation en T ou T*. Les séries 11 (47 poids) et 13 (56 poids) y sont particulièrement bien représentées et leur existence n'est donc pas douteuse.

- Des 55 cases prévues pour les poids de plus de 80 g (qui valent donc au moins 320 T*), 14 seulement ne sont pas occupées. Il y avait donc bien des poids inconnus des européens dont la table de multiplication akan permet de prédire l'existence.

- On dénombre 114 poids dans les lignes 48, 96, 192 etc. soit 38% des poids de chef. Leur petit nombre dans les sources européennes semble bien relever d'un biais, potentiellement lié à l'usage des piles de poids.

Tableau 6. Répartition des 298 poids de chef selon la table de multiplication akan. En rouge, le nombre de poids > 80 g par case.

5- Comment les Akan ont pu, sans numération écrite, faire des calculs aussi compliqués ?

Leur langue leur permettait, avec beaucoup de circonlocutions, de formuler des nombres supérieurs à 100 ¹³, mais comment effectuaient-ils des opérations aussi compliquées que 13 x 192 = 2496 en l'absence de support écrit ? Comment transmettaient-ils leur savoir ? Peut-on considérer avec Abel que les décors des poids géométriques aient eu une signification numérique ? Nous pensons que c'est le cas, et nous sommes en mesure de déchiffrer de nombreux poids, mais nous n'avons pu mettre en évidence aucune structure reproductible dans leur codage, qui s'apparente plus à un rébus qu'à une numération ordonnée. Nous ne savons pas comment ils faisaient, mais nous savons qu'ils l'ont fait puisque les poids sont là pour en témoigner, et que nous avons prouvé que la structure du système dont ils participaient ne devait rien au hasard.

Une façon de circonscrire le problème est d'évaluer le nombre de personnes concernées. Sur une population de 1 400 000 Akan, Garrard évaluait les possesseurs de poids à la veille de la colonisation à 60 000, se partageant une production cumulée au fil des siècles de trois millions de poids, soit une cinquantaine chacun, et le nombre de fondeurs en activité à une centaine. Il s'agissait donc d'une élite sociale et professionnelle. Si les possesseurs de poids devaient facilement en mémoriser la valeur, les fondeurs, dont Garrard estime la production annuelle à 100 poids, pouvaient être les seuls à en connaître toutes les subtilités.

On peut néanmoins se demander si cette table de multiplication a vraiment été utilisée en tant que moyen de calcul et s'il ne s'agit pas d'un artéfact mathématique, lié à la structure géométrique des séries de poids, qui apparaît quand nous les transposons dans notre système numérique. Si tel était le cas, cela ouvrirait la possibilité de modes de calcul alternatifs, comme les ethno-mathématiciens en ont étudié par exemple chez les Siamou au Burkina-Fiaso (Traoré, 2008). Mais cela ne retire rien à la valeur de ce que nous avons appelé la table de multiplication akan comme outil pour démêler l'écheveau des poids à peser l'or des Akan.

Conclusion

Cet article nous a permis d'expliquer comment nous avons construit la table de multiplication akan à partir de multiples sources, d'en détailler les subtilités et d'en discuter la pertinence. Il n'est pas in fine exclu qu'elle ne soit le fruit d'un biais mathématique que nous ne sommes pas qualifiés pour démontrer. Mais, puisque c'est aux prédictions qu'elle permet de faire qu'on juge la qualité d'une théorie scientifique, nous considérons que cet outil, avec lequel nous avons à la fois prouvé le dualisme du système pondéral Akan et prédit la répartition des poids de chef, est le mieux adapté à le décrire, sauf à découvrir comment les Akan auraient procédé autrement pour calculer leurs poids. La parole est aux ethno-mathématiciens.

Références bibliographiques

Abel H., 1952-1959. Déchiffrement des poids à peser l'or en Côte d'Ivoire. Journal de la Société des Africanistes, 22 : 95-114 (1952) ; 24 : 7-23 (1954) ; 29 : 273-286 (1959).

Binger L. G., 1892. Du Niger au Golfe de Guinée par le pays de Kong et le Mossi. Paris, Hachette, 2 vol. (vol. premier, 513 p. ; vol. second, 414 p.).

Bowdich T. E., 1819. Mission from Cape Coast Castle to Ashantee, with a statistical account of that kingdom, and geographical notices of other parts of the Interior of Africa. London, John Murray, 512 p. [Ed. Frank Cass, 1966].

Crappier J.-J., Farinetto C., Gascou P., Maunoury C., Maunoury F. & Mateusen G., 2019. The Akan Weighing System restored after 120 years of oblivion. A metrological study of 9301 geometric gold-weights. Colligo, 2(2). https://perma.cc/H494-E42R

De Marees P., 1605. Description et récit historial du riche royaume d'or de Gunea (sic), aultrement nommé, la coste d'or de Mina, gisante en certain endroict d'Africque. Amsterdam, chez Cornille Claesson, 100 p. [Les éditions Chapitre.com, 2017]

Garrard T. F., 1980. Akan weights and the gold trade. Legon history series. London, Longman, 393 p.

Mollat H., 2003. A new look at the akan gold weights of west Africa. Anthropos, 98: 31-40.

Niangoran-Bouah G., 1984-1987. L'univers Akan des poids à peser l'or. Dakar, Nouvelles Éditions Africaines, 3 vol. (Vol. I: Les poids non figuratifs, 1984, 316 p. ; vol. II: Les poids figuratifs, 1985, 320 p. ; vol. III: Les poids dans la société, 1987, 328 p.

Ott A., 1968. Akan gold weights. Transactions of the Historical Society of Ghana, 9: 17-42.

Traoré K. & Bednarz N., 2008. Mathématiques construites en contexte : une analyse du système de numération oral utilisé par les Siamous au Burkina Faso. Nordic Journal of African Studies, 17 (3) : 175–197.

Zeller R., 1913. Die goldgewichte von Asante (westafrika) eine ethnologische Studie. Leipzig, Teubner ed, 77 p.

Annexes

Annexe 1 : les différentes numérations akan (Bowdich, 1819)

Annexe 2 : la table IV de Zeller

Annexe 3 : les quatre séries de Garrard

D'après Garrard, p. 240-241.

Annexe 4 : listes de poids ashanti et akyem selon Garrard

Appellations Akyem et Ashanti. D'après Garrard, p. 347-349. Sur la base de 3£ 12 s pour une once troy. Les suffixes numériques ont été normalisés suivant les indications du tableau 1.

Annexe 5 : appellations Agni pour selon Binger

Annexe 6 : la table d'Abel

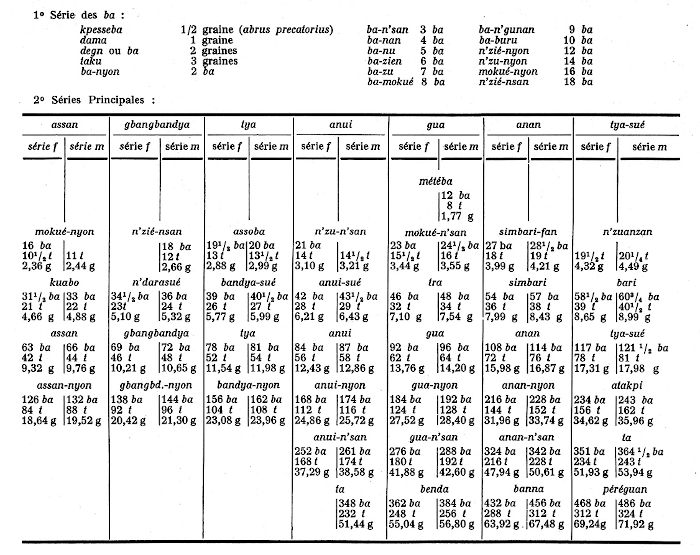
Les appellations sont Baoulé. Cette table est compliquée par la présence des valeurs mâles (séries m) et femelles (séries f), dont la différence est trop faible pour être opérante. Elle est de plus bancale car Abel ne prend pas comme base la suite 1, 3, 5… 13 taku, mais des valeurs moyennes, celles dont les noms sont les plus utilisés avec leurs multiples et sous-multiples. Cela donne une progression irrégulière, passant en taku d'une raison 6 à une raison 8 comme suit : 42 (assan), 48 (gbangbandya), 52 (tya), 56 (anui), 64 (gua), 72 (anan), 80 (tyasué). De plus, ces poids ne devraient pas se trouver sur une même ligne puisqu'ils ne sont pas multiples les uns des autres.

La table devient cohérente quand on la reconstruit en ba, en prenant comme unité de base 1, 3, 5… 13 ba et en changeant l'ordre des colonnes (Tableau 5). En ba plutôt qu'en taku car plusieurs noms de poids de la première ligne montrent qu'ils sont multiples du ba (mokué-nyon = 16, n'zié-nsan = 18, n'zu n'san = 21, mokué n'san = 24.

Annexe 7 : la Table de Multiplication Akan

1. Tokoo, takou, takoi ou tekkoo. ⇧
   

2. Akye, ackie, acquay ou akee. ⇧
   

3. Benna, banna ou benda. ⇧
   

4. Nom donné par les Anglais à la colonie qui deviendra le Ghana. ⇧
   

5. Damma, dont 2 font un ba, bien qu'il ne cite pas cette dernière unité. ⇧
   

6. Mithqal, mitiqal or mitkal. ⇧
   

7. Monnaie arabe d'un poids canonique de 4,25 g d'or presque pur. ⇧
   

8. Puisqu'il ne le décrivait qu'au sein du système faible, le seul qu'il connaissait, avec une marge insuffisante pour être opératoire (Annexe 6). ⇧
   

9. Sur la piste des graines. ⇧
   

10. Pour certains ce serait achtjen, le 1/16 d'une once de Cologne, en hollandais (Muller, 1673), pour d'autres ce serait la graine d'un arbre appelé ackée (Ott, 1968). Une autre hypothèse rattache agira au giratu, un poids mandé. ⇧
    

11. Voir Histoire de taku et de mitqal. ⇧
    

12. Ces piles sont des emboîtements de godets, dont chacun fait la moitié du précédent. On trouve couramment des godets de 1, 2 voire 4 Ozt, et leurs divisions, dans les collections de poids. ⇧
    

13. Aux nombres du Tableau 1, on peut rajouter oha=100 et apem=1000 en Ashanti. 2496 se dirait dans notre numération simplifiée : Ahem-no ne oha-nan ne buru-otwe ne asia, ce qui n'est pas simple. ⇧
    

Jean-Jacques Crappier
Collectionneur, Le Mans, France.
Email: Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.

Pierre Gascou
Ingénieur, Collectionneur, Versailles, France.