Vol. 2/2 | 2019 | Crappier et al. (fr)

Précis, sophistiqué, compliqué mais fonctionnel, ce système de poids africains, utilisé par les Akan jusqu’à leur colonisation pour payer en poudre d’or, est totalement passé sous les radars de la recherche ethnographique. Il faut dire que sa complexité n’encourageait guère à s’y intéresser, d’autant que l’affaire semblait résolue depuis 1980 par Timothy Garrard pour qui les Akan l’avaient appris des Arabes par les Dioula, caste de marchands africains islamisés, qui commerçaient avec les deux parties dans le cadre de la traite transsaharienne. L’étude d’une série de 9301 poids, dont 298 poids de plus de 80 g, vient contredire cette théorie au profit de celle d’un système autochtone, basé sur des graines et rigoureusement structuré, dans lequel les échanges se faisaient vraisemblablement grâce à un double jeu de poids faibles et de poids forts, permettant des transactions à prix constant mais poids variable. Le fort niveau de preuve de cette étude métrologique pose le problème de savoir comment les Akan ont pu, avec des techniques rudimentaires, développer, perpétuer et transmettre oralement, pendant des siècles, dans un espace politique morcelé, un système aussi sophistiqué ?

Mots clés : Monnaies africaines - protomonnaies - poids à peser l’or - système pondéral - Akan - Ashanti - Baoulé - Abel Henri - Garrard Timothy - Ba - Taku

Precise, sophisticated, complicated but functional, this weighing system, used by the Akan until their colonization to pay in gold powder, has been little studied by ethnologists. One must say that its complexity did not encourage much interest, especially since the discussion seemed to have been closed in 1980 by Timothy Garrard, for whom the Akan had learned their weighing system from the Arabs by the Dioula, caste of African merchants who traded with both sides in the context of the trans-Saharan trade. The study of a series of 9,301 weights, including 298 weights over 80 g, contradicts this theory in favor of an aboriginal system, based on seeds and rigorously structured, in which exchanges were probably made thanks to a double set of light and heavy weights allowing transactions at constant price but variable weight. The high level of proof of this metrological study questions the way in which the Akan were able, with rudimentary techniques, to develop, perpetuate and transmit, orally, for centuries, in a fragmented political space, such a sophisticated system?

Keywords: African Currencies - Goldweights - Gold Weight - Weighing System - Akan - Ashanti - Baule - Abel Henri - Garrard Timothy - Ba - Taku

Introduction

Les Akan, qui vivent en Afrique entre Côte d’Ivoire et Ghana, ont développé pendant plus de 600 ans une civilisation brillante dans laquelle l’or jouait un rôle central comme symbole de beauté, de richesse et de pouvoir. Utilisant la poudre d’or comme monnaie de tous les jours, ils ont inventé, pour leurs échanges, un système de poids d’une sophistication unique au monde, allant, par leur valeur symbolique, bien au-delà de simples moyens de pesée et de paiement.

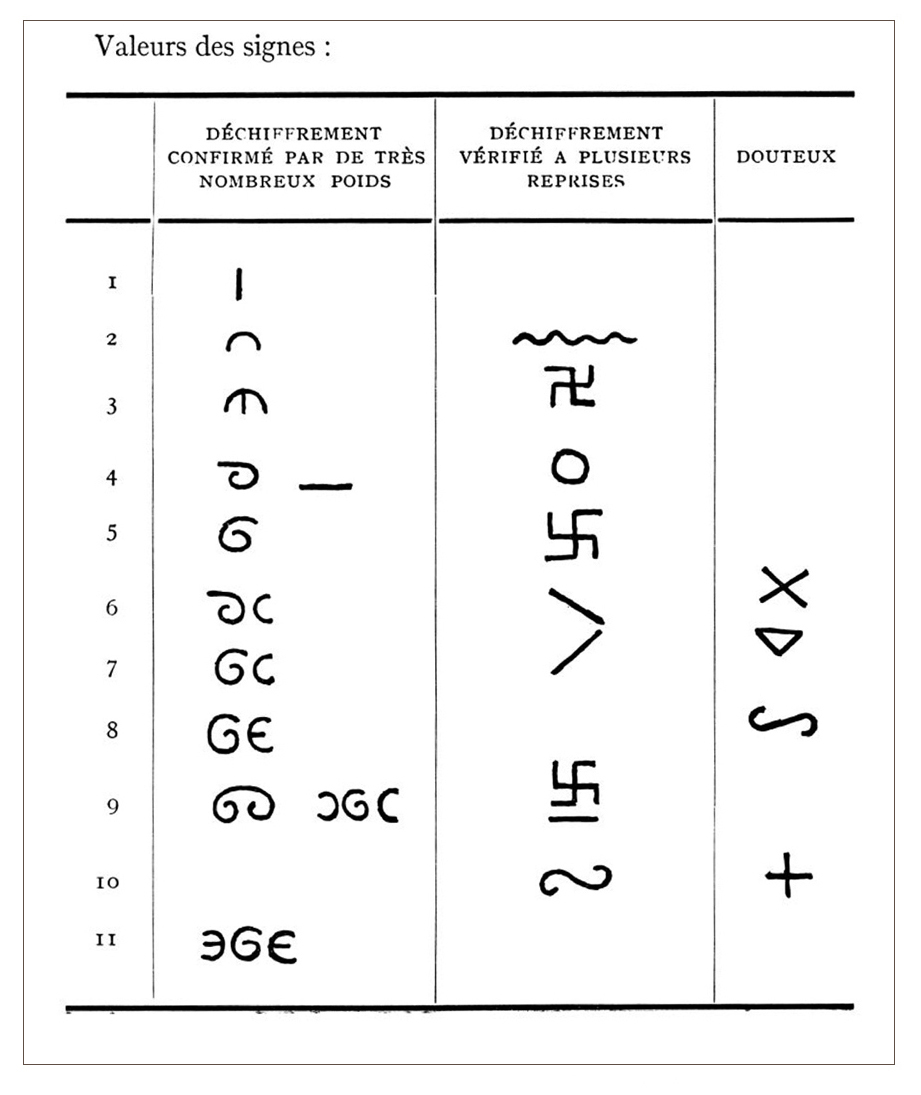
Figuratifs ou de formes géométriques, ils ont été peu étudiés par les spécialistes des cultures africaines et leur signification reste mystérieuse, bien que nous disposions des informations recueillies par des générations de marchands et d’explorateurs et des milliers de poids qui se trouvent dans les collections des musées et des particuliers. Quelques rares chercheurs ont essayé d’en percer le mystère à partir des récits anciens, de données de terrain et d’études métrologiques.

Rudolph Zeller, le premier, décrit en 1912 (Zeller, 1912), à partir d’informations recueillies au Ghana, un système basé sur une graine, le taku ¹, d’un poids de 0,25 g. Très complexe, il est organisé en 7 séries parallèles dont le premier poids est respectivement 1,3,5,7,9,11 ou 13 taku, et dont les suivants sont une succession de multiples par 2.

Ses travaux sont repris en 1952 par Henri Abel, en Côte d’ivoire, qui introduit une seconde graine, le ba ², d’un poids calculé de 0,146 g, dans un rapport de 3 pour 2 avec le taku, dont il réévalue le poids à 0,22 g (Abel, 1952) ³. Il introduit aussi la notion d’un système dualiste « poids mâles - poids femelles » ⁴ permettant des transactions à prix constant mais poids variable, dans lequel vous revendez ce que vous avez payé en or au même prix, mais en quantité moindre, la différence représentant votre bénéfice, ou votre intérêt dans le cas d’un prêt. Abel, convaincu que le décor des poids avait une valeur numérique, en avait proposé une grille de décodage (Fig. 1).

Fig. 1. Grille de décodage d'Abel. D'après Antonie Abel (1973)

En 1968, Albert Ott, au Ghana, constate l’existence de deux systèmes de poids distincts, correspondant in fine aux deux valeurs du taku, mais il les considère comme un moyen d’échange entre les différentes nations akan (Ott, 1968). En 1980, Timothy Garrard, au Ghana, dans une étude très documentée, fondée sur la pesée de 3000 poids, théorise l’adoption, par les Akan, du système pondéral arabe dont l’unité de base est le mitqal, le poids d’un dinar en or, qu’il évalue à 4,4 g ⁵. Par la suite, une fois le contact établi avec les européens, les Akan auraient successivement intégré à leur système les poids portugais, hollandais puis anglais. Il dénombre 62 unités qu’il classe, avec de larges marges de tolérance en quatre séries, deux d’origine arabe, l’une fondée sur le mitqal, l’autre sur l’uqiya (once de 26,4 g), les deux autres sur les poids portugais et anglais (Tableau 1). Garrard, qui connaissait les travaux de ses prédécesseurs, n’accordait qu’un rôle secondaire aux graines, rejetait comme fantaisiste le décodage des poids, et comme infondée l’hypothèse d’un système dualiste. Cette thèse, bien que partiellement mise en doute, est celle qui fait actuellement autorité.

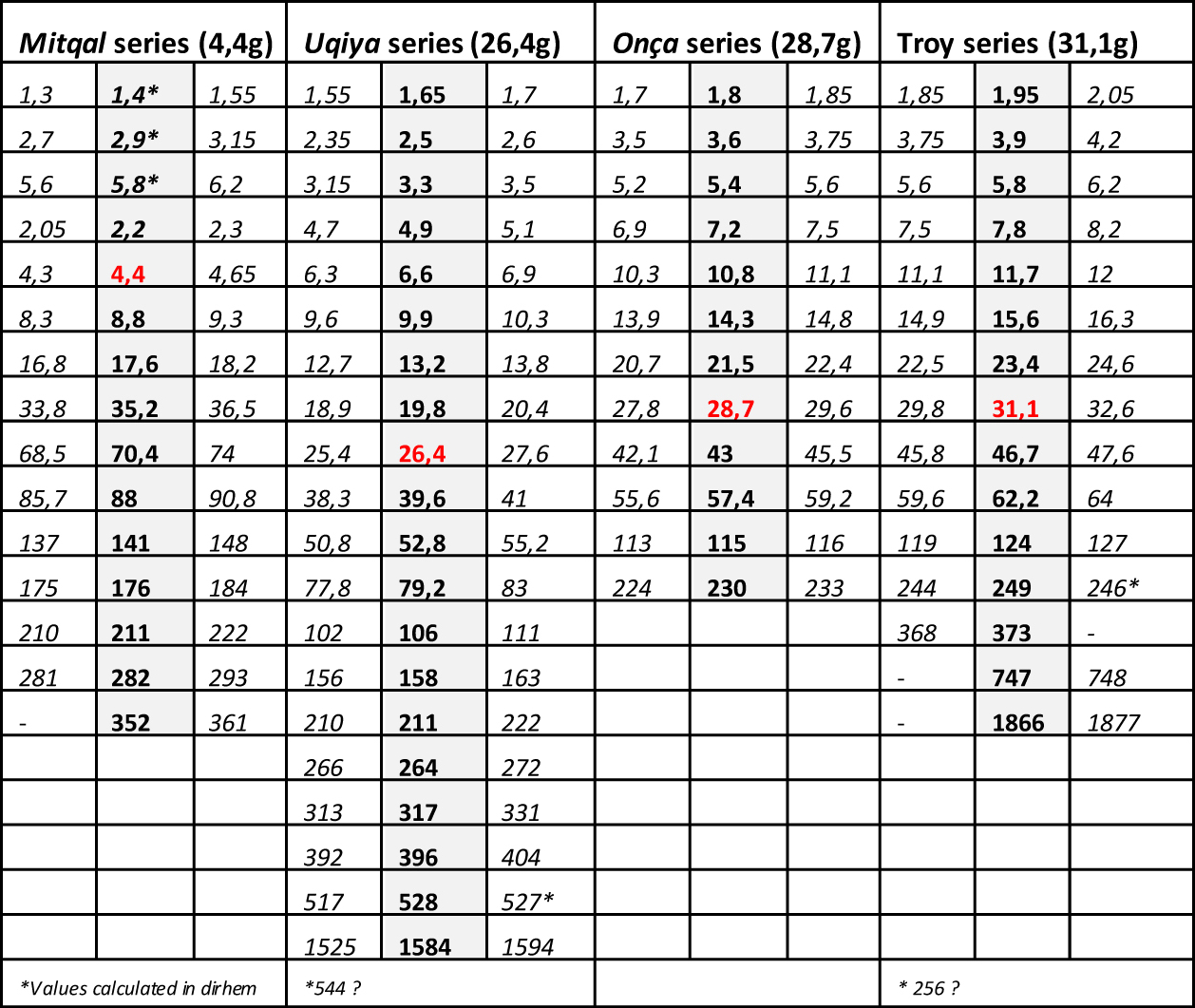
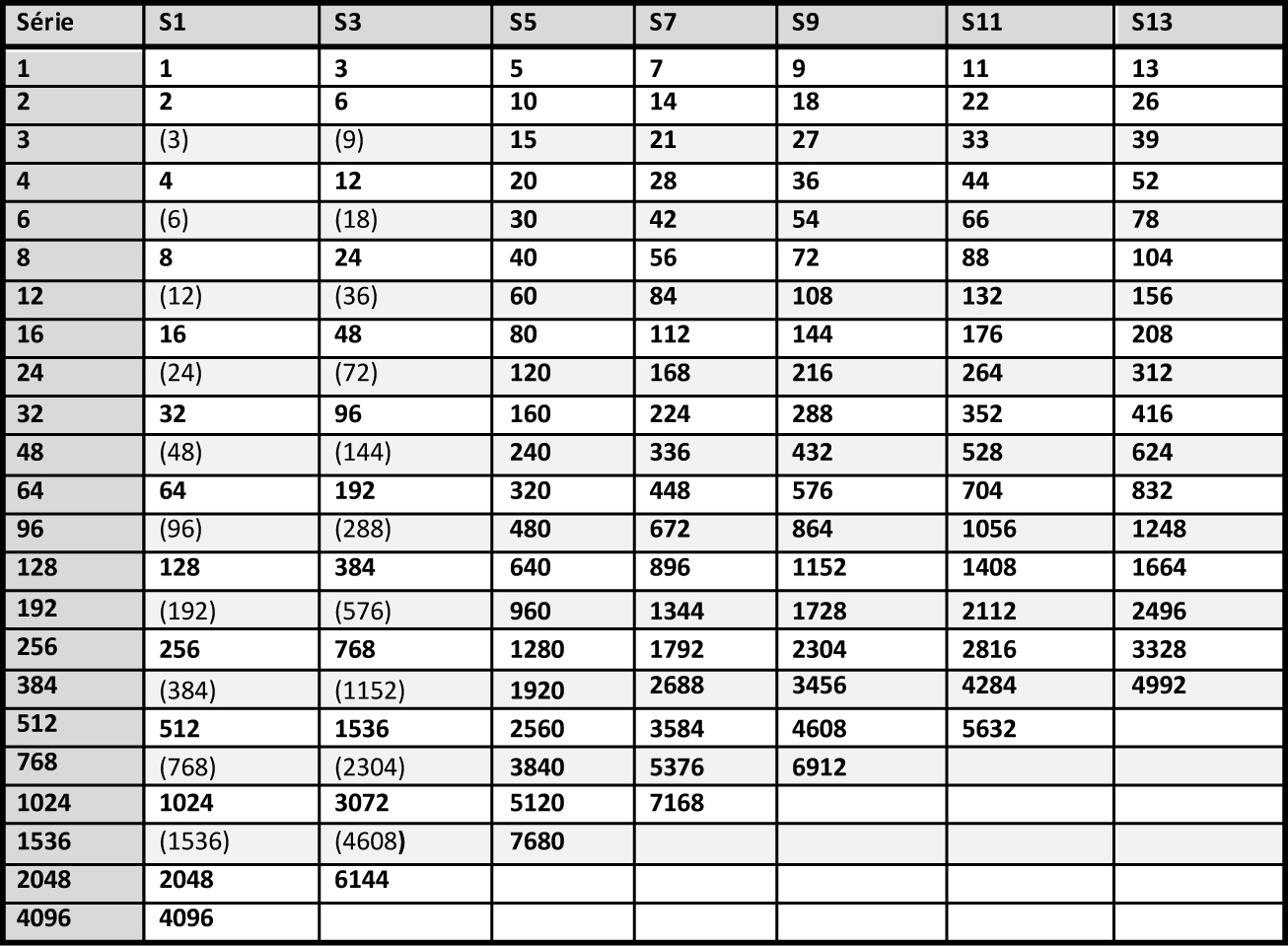
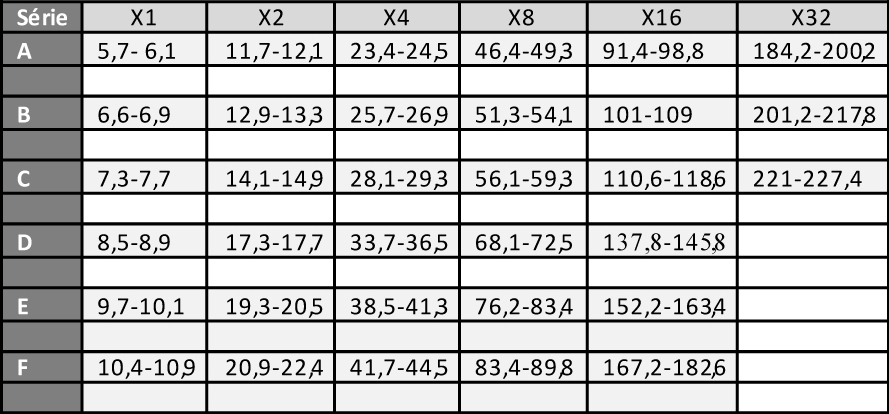
En 1987, Georges Niangoran-Bouah, ethnologue ivoirien, reprend la thèse d’un système dualiste, qu’il dit être encore en vigueur à cette époque sur les marchés d’Abidjan, mais sans aller plus loin dans la démonstration (Niangoran-Bouah, 1987).

En 2003, Harmut Mollat, fort d’une étude de 3800 poids, remet partiellement en cause la thèse de Garrard, en contestant la matérialité des séries d’origine européenne et le rôle pondéral des poids figuratifs, mais en garde l’essentiel, c’est-à-dire le rôle central du mitqal et celui, marginal, du taku (évalué à 0,25 g).

Mais la théorie de Garrard, même corrigée par Mollat, n’est pas cohérente avec les listes de poids qu’il rapporte lui-même dans son livre. Recueillies dans les différents états akan auprès de notables âgés, établies en monnaie anglaise, aucune ne cite le mitqal mais toutes font état du taku, évalué à 6 pence, ce qui, au cours de 8,8 g d’or akan pour une £, cité par les mêmes informateurs, lui donne le poids de 0,22 g. Garrard n'a pas tenu compte de ces listes dans sa démonstration. C’est pour nous l’origine de son erreur, et l’indice que le poids de 4,4 g dont il fait la pierre angulaire de sa théorie, n’est pas un mitqal ⁶, africanisé, mais simplement la contre-valeur de 10 shilling, et donc le vingtuple du taku léger d’Abel dont l’existence se trouve ainsi confortée.

Hypothèse dualiste :
Nous proposons de faire la synthèse de ce qui précède en combinant ces 2 taku dans un système dualiste, comme Abel, mais dans lequel les poids faibles reposeraient sur le taku de 0,22 g que nous appellerons T, les poids forts sur le taku de 0,25 g que nous appellerons T*. La différence de 12% entre les deux représentant une marge bénéficiaire acceptable dans un monde ne connaissant ni la TVA ni les charges sociales. Il faut pour être complet y rajouter deux autres unités, le ba léger de 0,14 g, déjà connu, et un ba fort de 0,16 g dont on trouve trace dans le rapport que Louis Gustave Binger fait des poids en pays Agni (Binger, 1892). T et T* sont toujours dans un rapport de 2 pour 3 avec B et B*

En compilant les diverses listes de poids que nous ont légué des marchands européens dès le 16^e siècle, en décortiquant la structure de leurs appellations akan, on construit, sur le modèle de Zeller, l’ossature de ce système, sous la forme d’une table de multiplication (Tableau 2). Complexe, elle comporte une centaine de cases, correspondant aux têtes de séries de Zeller (1,3,5,7,9,11 et 13) multipliées par 2,4,8,16 etc. mais aussi par 3,6,12,24, 48 etc. Reportez-vous au Tableau 2 pour la visualiser.

Il nous faut cependant envisager aussi une hypothèse plus triviale qui ferait de cette apparente complexité la conséquence, au fil des siècles et des échanges, de l’imbrication de systèmes régionaux, voire familiaux, dans lesquels seuls quelques poids, plus ou moins basés sur le mitqal et connus de leurs seuls possesseurs, auraient vraiment utilité pondérale, les autres pièces du dja ⁷ valant plutôt par leur caractère magique ou symbolique.

Méthode

Objectifs

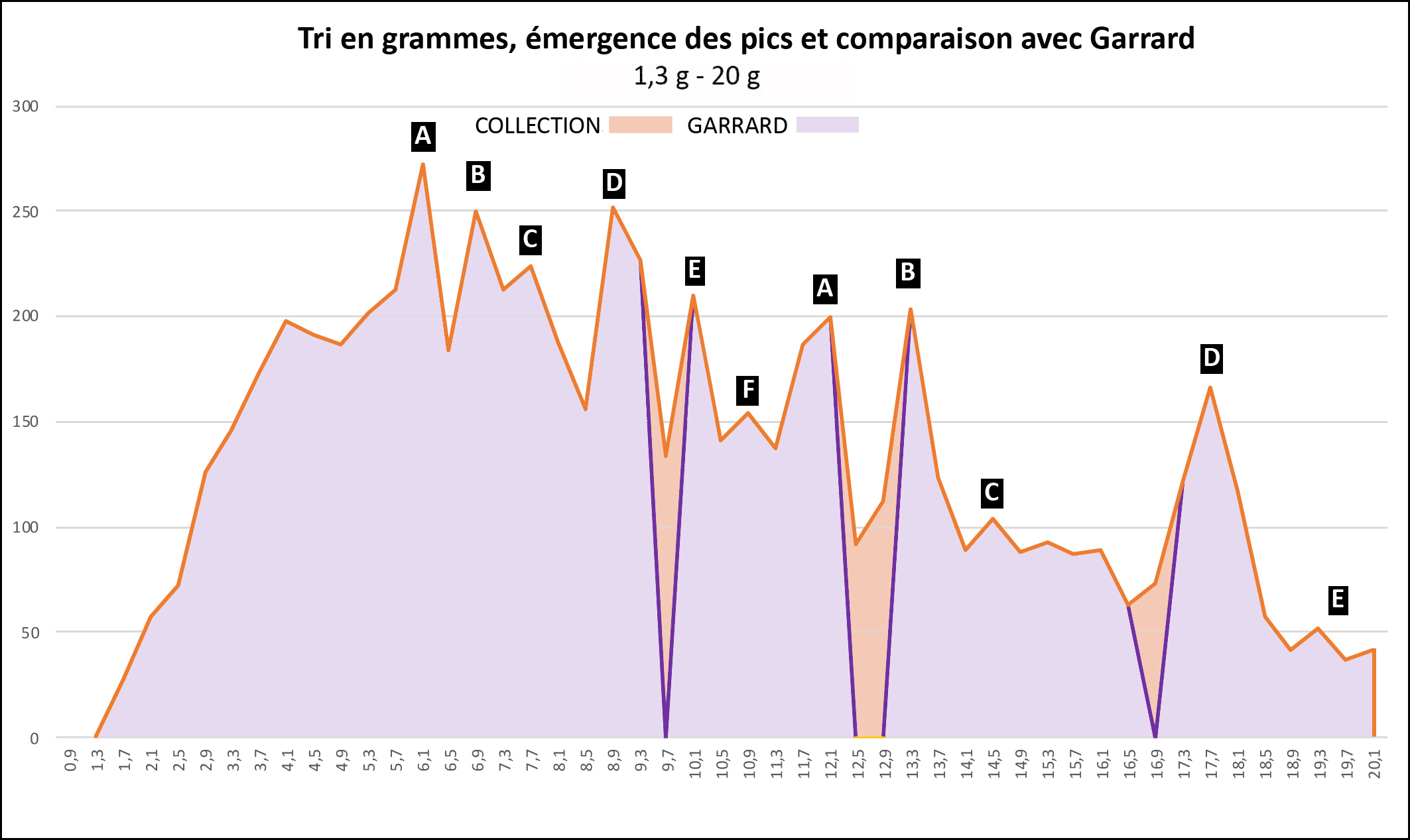
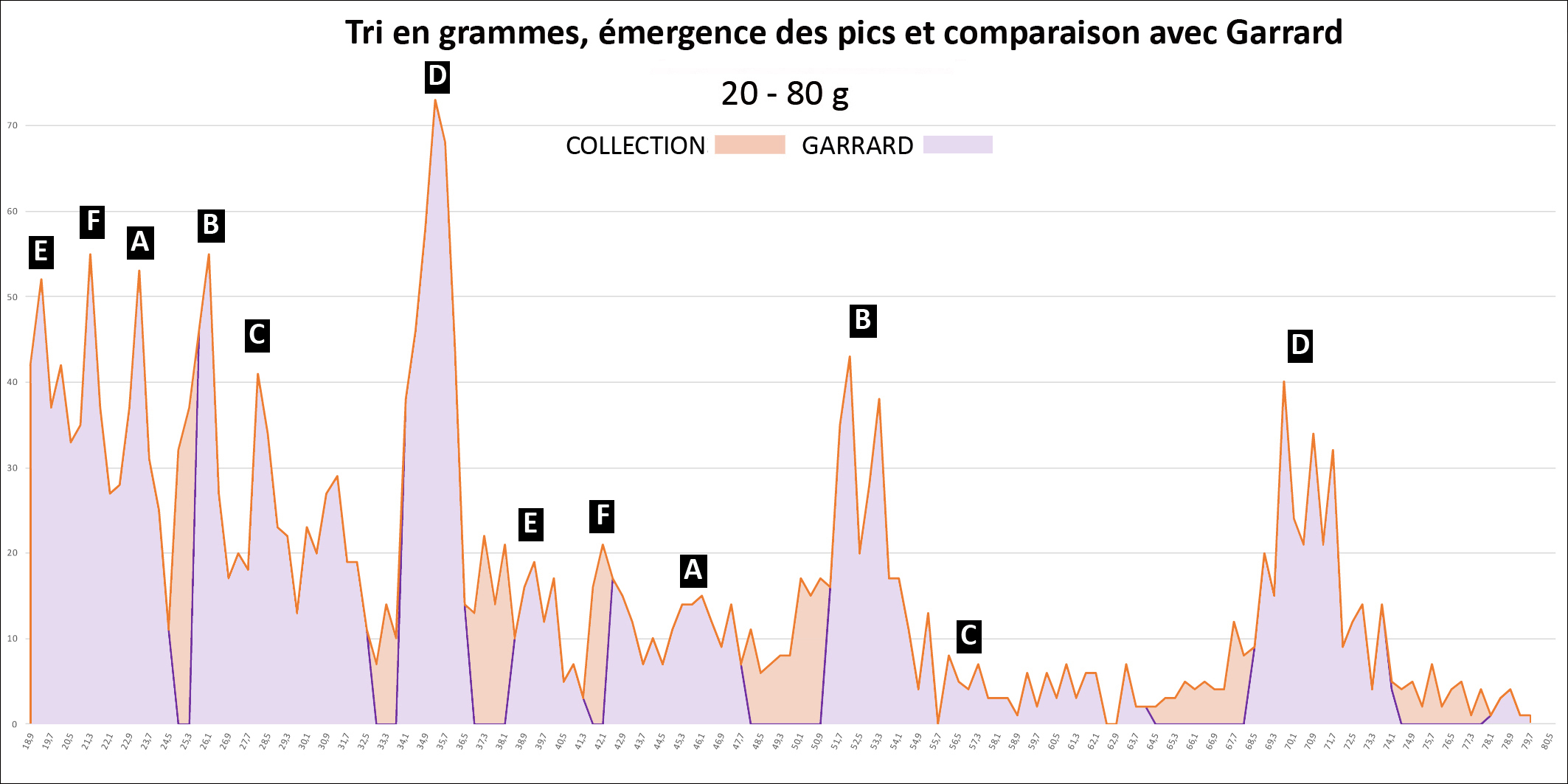
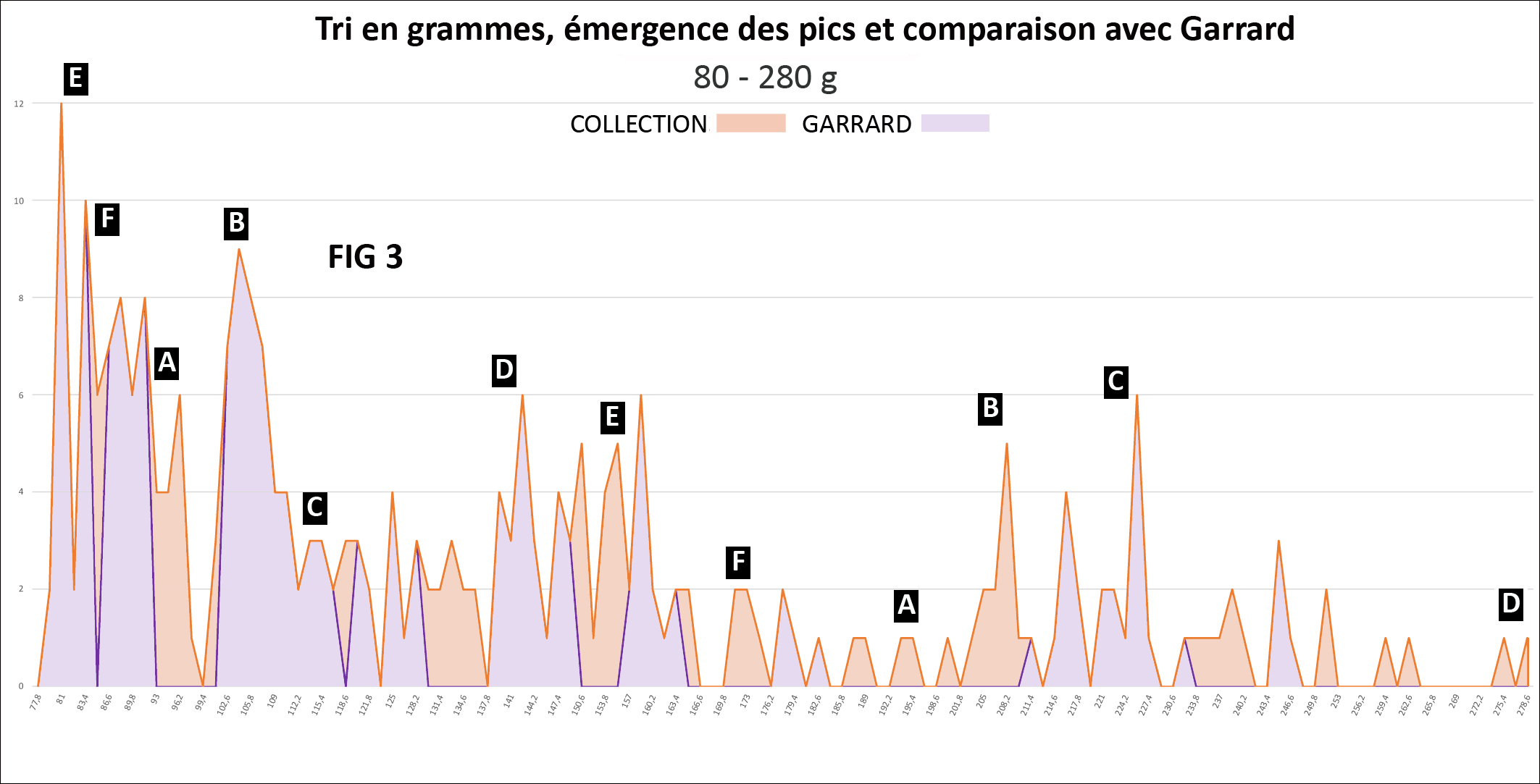
Pour étudier le système pondéral des Akan, nous avons colligé 9301 poids géométriques ⁸ de provenances diverses ⁹, allant de 1,3 g à 1900 g, dont 2420 pèsent de 20 à 80 g et 298 plus de 80 g. Malgré l’hétérogénéité de cet ensemble, nous voulons démontrer :
- que la distribution des poids qui la compose ne résulte pas d’une accumulation anarchique de variants locaux mais qu’elle est ordonnée ;
- que cet ordre est celui de la table de multiplication akan et non celui de Garrard ;
- qu’il relève de la théorie dualiste (T+T*) plutôt que de celles d’Abel ou Zeller, fondées respectivement sur le taku faible (T) et le taku fort (T*).

Critères de jugement

Si nous avons vu juste :

1) Les poids, après transformation dans le système faible ou fort correspondant, doivent s’inscrire dans une des cases de la table de multiplication avec, selon des expériences menées sur des balances akan, une précision minimum de ± 2%, en pratique de [-2,5% à +1,5%] pour tenir compte de leur usure. Le nombre de poids qui rentreront dans cette fourchette étroite sera notre critère de jugement pour valider la table de multiplication akan.

2) la théorie de Garrard devrait échouer à décrire notre collection avec autant de précision. De même que les théories d’Abel et de Zeller. Ce sera notre critère de jugement pour valider le système dualiste.

Nous avons traité notre collection avec un tableur Excel :

1) Tri en grammes :
Nous avons trié nos poids avec un incrément de 0,4 g jusqu’à 80 g, de 1,6 g au-delà. Nous avons analysé leur distribution et regardé celle que prévoyait la théorie de Garrard, selon les classes de tri qu’il décrit (série Garrard) mais aussi, pour plus de rigueur, selon la fourchette étroite (série Garrard bis).

2) Tri en taku:
Nous avons échoué à transformer les poids de moins de 80 g en taku, le recouvrement des marges empêchant de distinguer entre T et T*, mais avons pu le faire sur les 298 poids de plus de 80 g. Rares et réservés à l’élite, ces poids dits « poids de chef » sont considérés comme les plus précis. Leur nombre restreint, mais suffisant pour des calculs statistiques, a permis de les analyser un par un, de calculer leur valeur en taku léger et en taku lourd, et de leur assigner la case de la table de multiplication dont leur valeur est la plus proche ¹⁰, et en mesurant l’écart entre valeur observée et valeur standard. Nous avons de la même façon testé les hypothèses d’Abel et de Zeller et comparé les résultats.

Résultats

1) Tri en grammes

Distribution des poids :
Les Figures 2, 3 et 4 rendent compte de la distribution des poids de 1,3 à 280 g (tracés en orange).
- À partir de 6 g des pics s’individualisent dans un désordre apparent d’où émergent au moins 6 séries successives, notées de A à F, chacune suivant une progression géométrique de raison 2 dont l’ordonnancement est détaillé dans le tableau de la Figure 6. Les séries B et D correspondent aux valeurs des séries uqiya et mitqal de Garrard (Tableau 1).

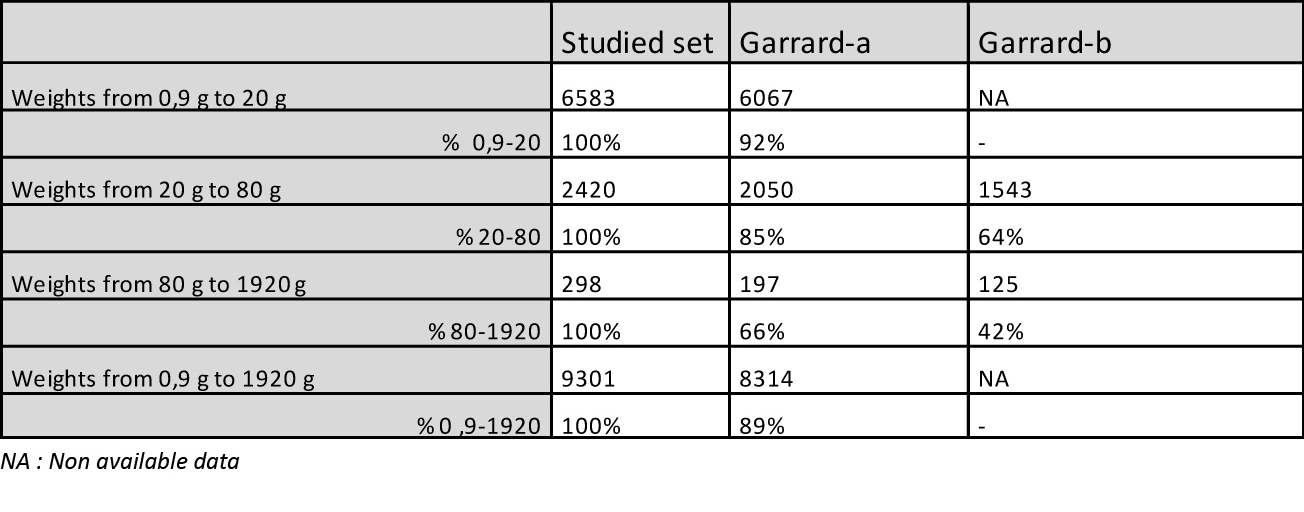
- Les graphiques montrent aussi comment devraient se répartir les poids s’ils obéissaient à la théorie de Garrard, selon ses classes de tri (tracé en violet). Les premières lacunes apparaissent dès 9,3 g. Elles sont visualisées sur les graphiques par les aires en orange clair.

- Le Tableau 4 montre que si la théorie de Garrard rend globalement compte de 89% des poids, entre 20 et 80 g, ce score baisse à 85% (2050/2420) et à 66% au-delà de 80 g (197/298) (colonne Garrard). Si on tient compte de la fourchette étroite (colonne Garrard bis), il baisse à 64% (1543/2420) et 42% (125 /298).

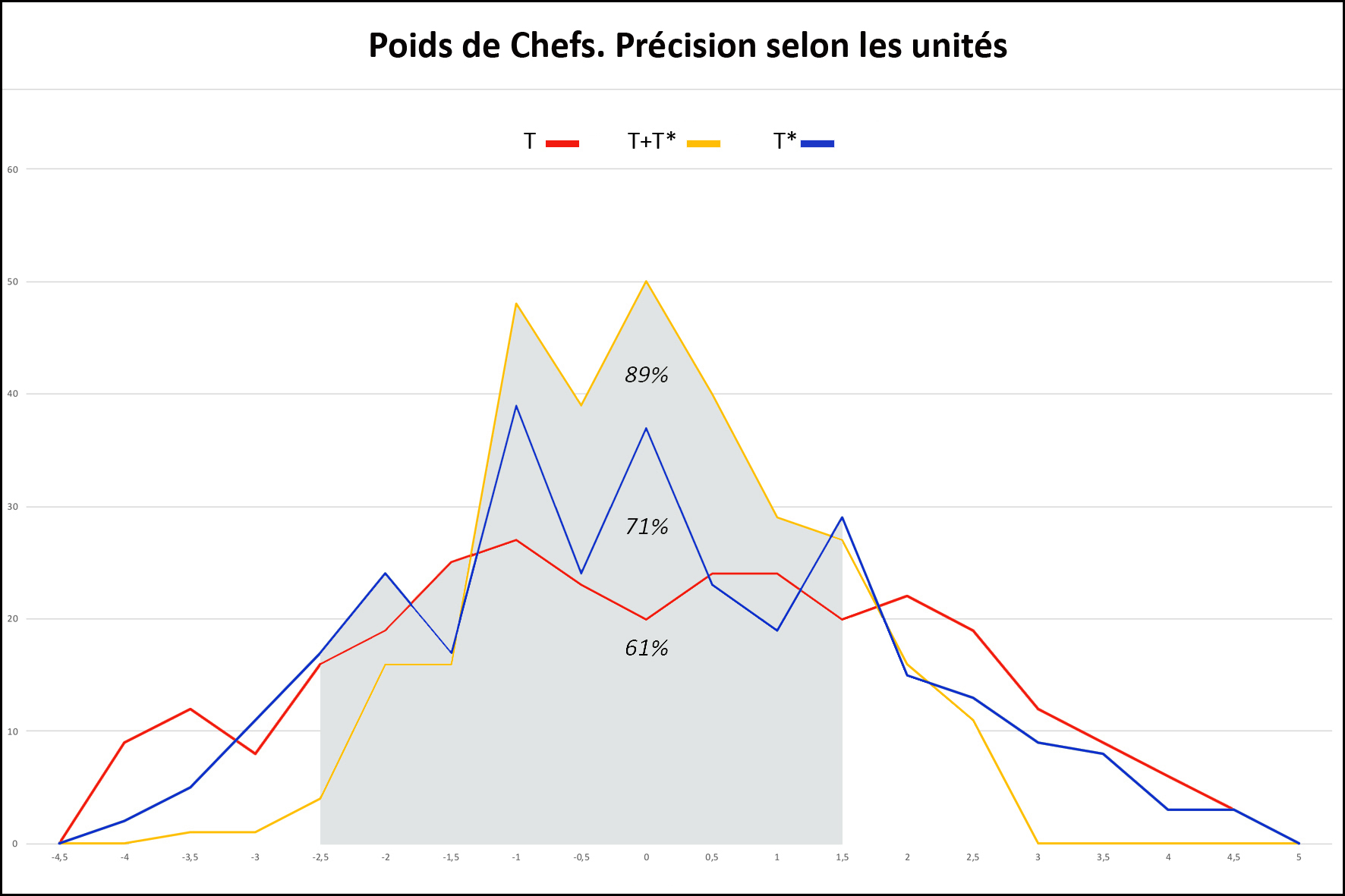
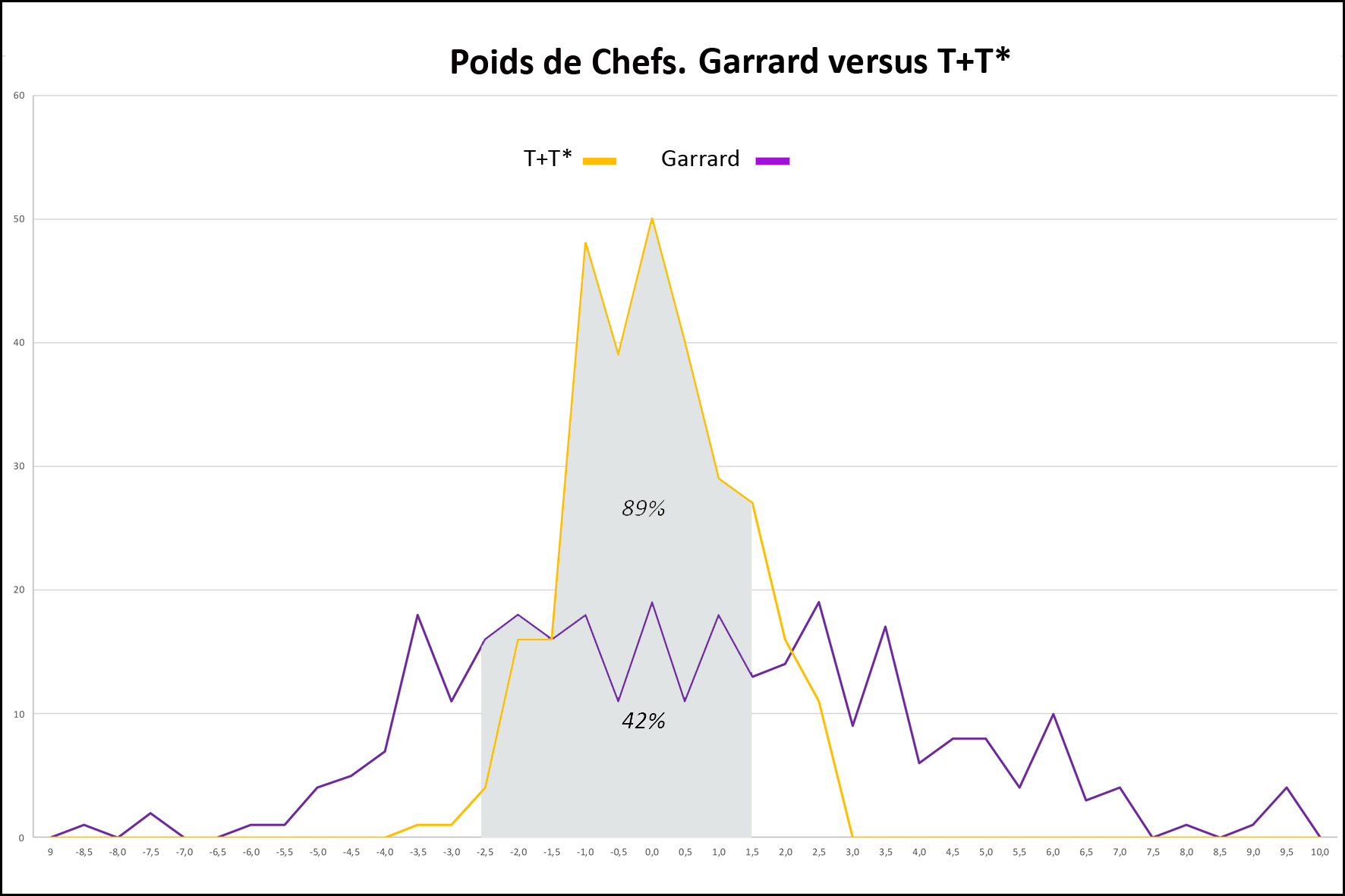
2) Tri en taku des 298 « poids de chef »

Les calculs n’ont été effectués qu’en taku pour des raisons que nous avons exposées.

-Les Figures 5 et 6 rendent compte du tri des poids de chef en taku sous forme d’histogramme empilés. Transformés en T ou T*, tous, sauf deux, trouvent leur place dans la table de multiplication.

- La Figure 7 compare les précisions obtenues selon les hypothèses T+T*, T seul, T* seul. Tous les poids s’intègrent dans la table dans une fourchette maximum de [-4% à +4,5%].

Dans l’hypothèse T+T*, 100% sont dans la fourchette [-4% et +2,5%], 94% entre [-2,5% et +2%]. Le critère de jugement [-2,5% à 1,5%], matérialisé par l’aire en gris sous les courbes, est satisfait par 89 % (265/298) des poids de chefs dans l’hypothèse T+T*, 71 % (212/298) dans l’hypothèse T* et 61% (182/298) dans T.

3) Tri des poids de chef. Garrard versus hypothèse dualiste

La Figure 8 confronte la précision que permet la grille de Garrard à celle de l’hypothèse dualiste. La courbe Garrard s’étale entre [-9% et +10%]. On retrouve les 125 poids (42%) du Tableau 4 correspondant à la fourchette étroite. 91 de ces 125 poids (73%) appartiennent aux séries mitqal ou uqiya, 18 (14%) à la série dite portugaise et 16 (13%) à la série anglaise.

Discussion

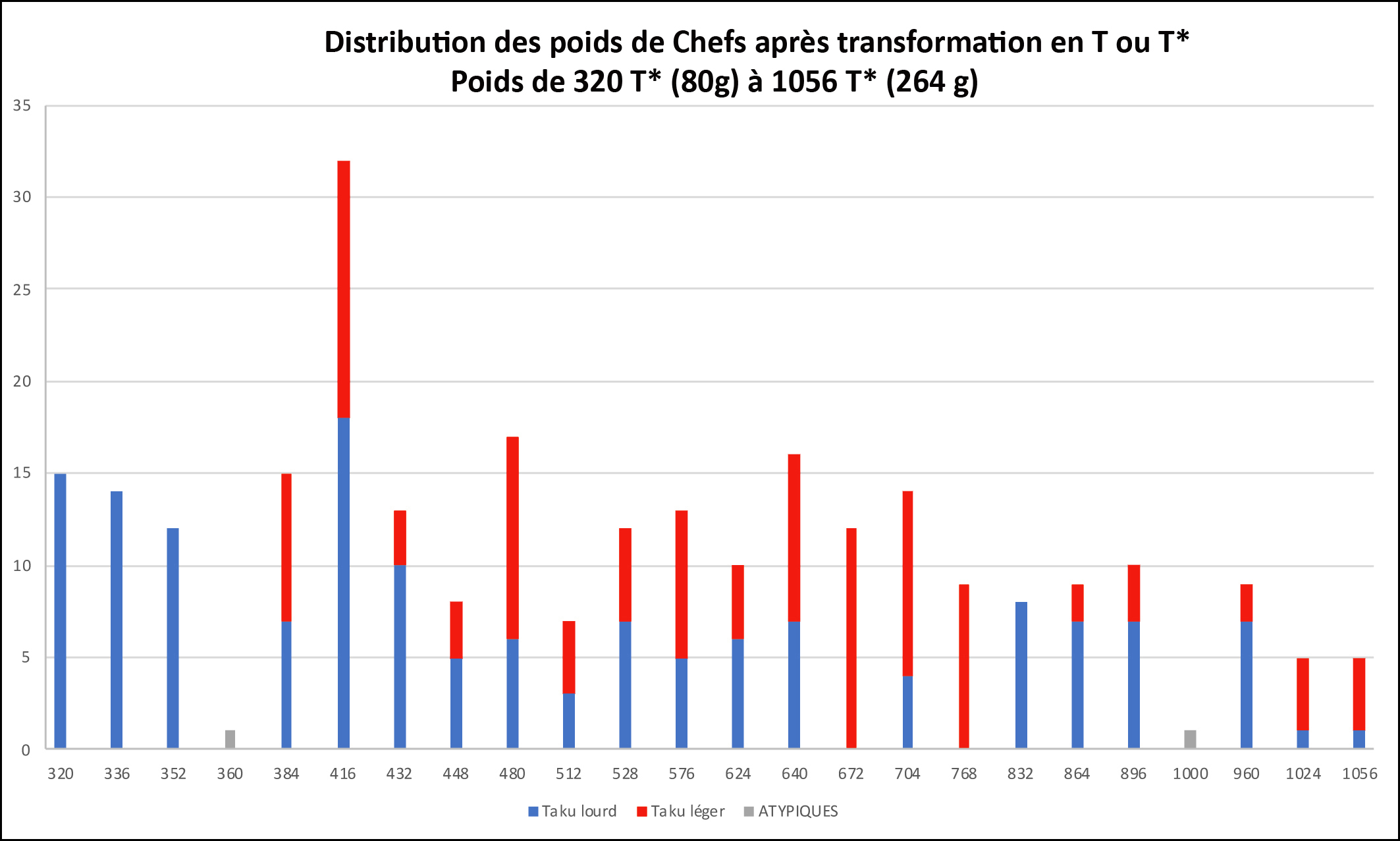
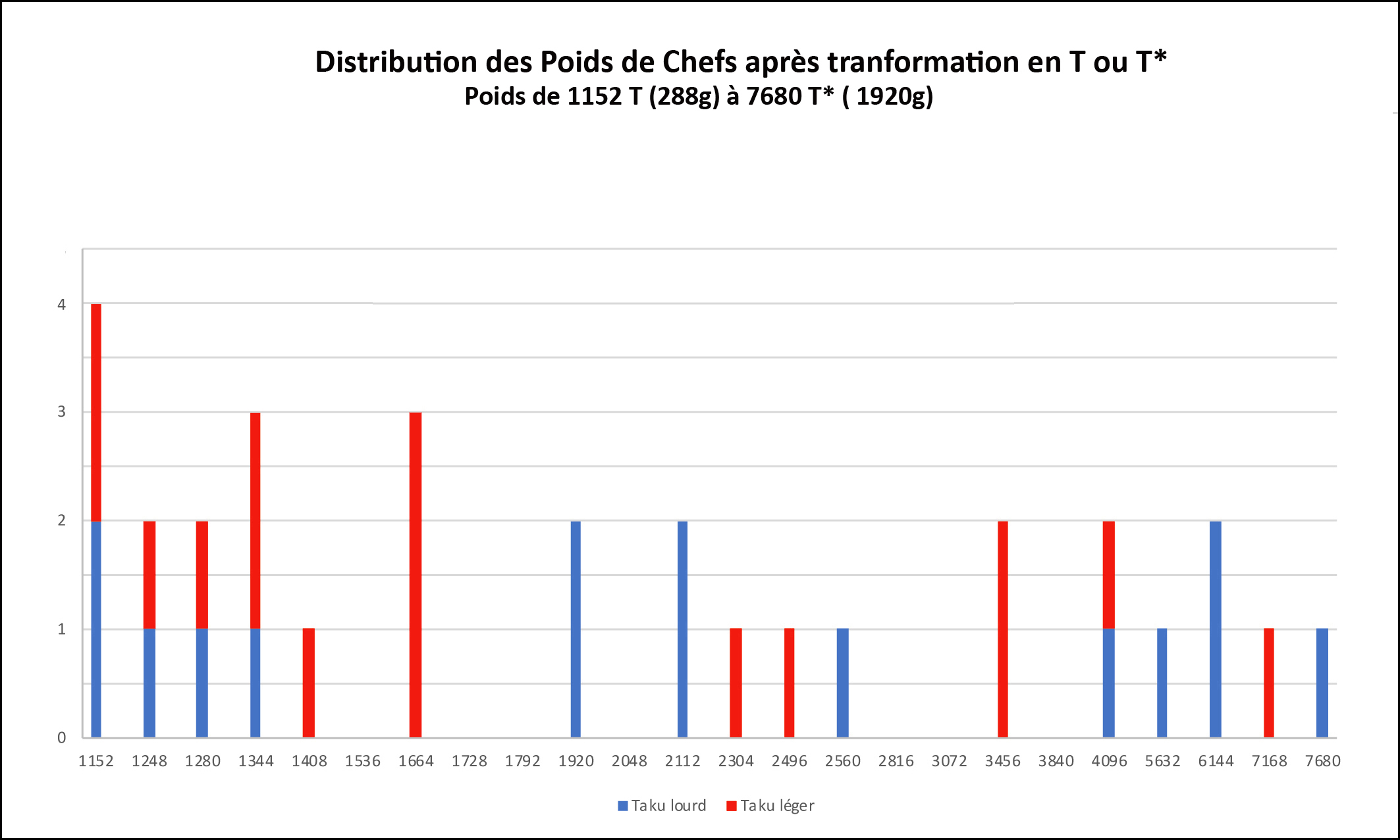
1) Que penser de notre collection de poids?

Il s’agit de la plus importante collection de poids géométriques jamais étudiée dont le point fort est la série de 298 poids de chef. Garrard n’avait réuni que 2000 poids, et Mollat 2500, avec très peu de valeurs >80g. Composée de poids de diverses origines et de tous âges, elle permet de montrer l’unicité du système pondéral akan dans le temps et dans l’espace. Bien loin d’une anarchie, elle en montre l’organisation rigoureuse, sous forme de séries de pics que l’on peut interpréter comme une succession de courbes de Gauss autour d’une valeur pivot, mais aussi, au vu de leur élargissement progressif, comme des ensembles composites, associant des valeurs en T et en T*.

2) Le résultat du tri des poids de chef valide-t-il la table de multiplication ?

Le résultat du tri dans le système T+T* est sans équivoque avec un score de 89%, passant à 94 % si on tolère une marge supérieure ≤2%. Étant donné les avatars que certains de ces poids ont connu, que la qualité parfois médiocre de notre documentation photographique ne permet pas toujours d’identifier, et la possibilité qu’il s’y soit glissé quelque faux, on peut parler de « quasi 100% ». Notre premier critère de jugement est donc rempli. Ces résultats valident la table de multiplication avec tout ce qui en découle sur les capacités de calcul des Akan.

3) Laquelle des 4 théories est favorisée par la comparaison des précisions ?

89% de précision pour T+ T* contre 71% pour T* et 61% pour T (Figure 7), les tests statistiques (voir Annexe) nous prouvant que ces différences sont significatives, on peut affirmer que la théorie dualiste rend mieux compte de la répartition des poids de chef que les théories de Zeller et d’Abel. Pour ces deux dernières le grand nombre de poids imprécis situés aux extrêmes de la courbe est le signe qu’ils appartiennent à l’autre catégorie.

La théorie de Garrard est celle qui décrit le plus mal notre collection. Le tri en gramme montre qu’elle diverge d’autant plus de la réalité qu’on progresse en poids et en précision. On remarque que si les séries B et D correspondent respectivement aux séries uqiya et mitqal de Garrard, elles correspondent tout autant dans la table de multiplication aux multiples par 3,6,12 etc. et 2,4,8 etc. du taku léger (Tableau 2).

Avec seulement 125 poids (42%) dans la fourchette [-2,5% à 1,5%], c’est aussi la théorie dont la précision est la plus mauvaise quand elle passe au révélateur des poids de chef. De plus, l’analyse de ces 125 poids montre que 73% appartiennent aux séries islamiques et 14% à la série portugaise, séries relevant en fait du système faible. On peut donc dire qu’il s’agit en quelque sorte d’une théorie T dégradée. Notre second critère de jugement est donc rempli, ce qui valide la dualité des poids, mais l’hétérogénéité spatio-temporelle de notre collection ne nous permet pas d’affirmer qu’il s’agisse d’un système dualiste intégré plutôt que deux systèmes, l’un en T, l’autre en T*, géographiquement séparés.

Décédé prématurément, Garrard ne peut pas répondre à nos critiques. Comment expliquer qu’il se soit trompé malgré son érudition et la pertinence de son analyse historique ? Nous y voyons la conséquence de l’acculturation de ses informateurs, qui, bien que très âgés, n’avaient vraisemblablement jamais utilisé eux-même les poids, ou alors dans un système déjà dégradé et inféodé aux poids et monnaies britanniques, où les transactions ne se faisaient que dans le système faible. Ils n’en connaissaient pas, ou plus, toutes les subtilités, ces histoires de poids mâles et femelles, ni le rôle des graines. La théorie de Garrard expliquait, en forçant à peine, 90% des poids ; celle de Zeller était incomplète ; celle d’Abel était confuse ; 20 T sont très proche du mitqal ; il n’avait pas les outils informatiques pour manipuler sa collection ni suffisamment de poids de chef pour comprendre que sa théorie ne les expliquait pas. Il n’avait donc pas de raison d’en douter.

4) Quelles sont les graines sans lesquelles ce système ne pourrait fonctionner ?

Seule celle qui correspond au ba léger fait consensus. Le taku a gardé son mystère, mais une recherche sur Google avec, par analogie, « caroubier » comme mot-clé, nous conduit au néré, le caroubier africain, alias Parkia biglobosa, dont la graine est consommée par les Akan. D’un poids moyen de 0,25 g, elle ne pèse plus, une fois bouillie puis épluchée ¹², que 0,22 g ¹³, ce qui en fait un taku tout à fait convenable. Pour ce qui est d’Abrus precatorius, la solution vient d’Abel, qui nous apprend que selon qu’elle est cueillie en saison sèche ou humide, le poids moyen de sa graine, dont il faut 2 pour faire un ba, est de 74 mg ou 83 mg ¹⁴.

5) Comment expliquer que ce dualisme ait échappé à la curiosité des marchands européens ?

Vraisemblablement par la souplesse des poids akan, dont, par un effet du hasard, le système faible était en phase avec les poids arabes et portugais, tandis que le système fort s’appariait avec celui des Hollandais puis des Anglais ¹⁵. Les Akan, qui vérifiaient chaque transaction avec leurs poids, ont donc utilisé l’un ou l’autre système selon leur interlocuteur, qui ne pouvait donc en connaître que la partie qui le concernait. Cette dualité n’a d’ailleurs pas échappé à tout le monde, puisque Dapper (1686) et Barbot (1679 cité par Debien et al., 1979) en ont fait plus ou moins explicitement état.

6) Peut-on attribuer pareille précision à un système considéré comme empirique et magique ?

La réalité des chiffres est là qui prouve le degré d’organisation et de précision du système pondéral akan. Nous ne sommes pas dans le domaine de l’ethnologie, mais dans celui de la métrologie. Pour invraisemblable que ce soit, les Akan sont arrivés à concevoir des opérations complexes sans support écrit et à fabriquer des poids avec une précision quasi industrielle. Aux experts d’expliquer comment.

7) C’est volontairement que nous n’avons pas abordé le décodage des poids auquel Abel croyait sans avoir pu le prouver. Notre expérience nous a cependant montré qu’avec quelques modifications de sa grille, la possibilité de calculer dans l’un ou l’autre des deux systèmes en ba et taku, et l’introduction pour les poids les plus lourds de l’acke, une troisième unité d’une valeur de 8 taku ¹⁶, il est possible de décoder plus de 50% des poids, d’une façon relativement standardisée et en respectant scrupuleusement les valeurs de la table de multiplication. C’est ce qui a été possible de faire pour la moitié des poids de chef, sachant qu’une meilleure documentation photographique aurait amélioré ce score.

8) Dans cet exposé, certains points sont supposés comme acquis, ou sont brièvement résumés. Il s’agit de la façon dont a été établie la table de multiplication, des documents historiques qui soutiennent l’hypothèse d’un système dualiste, des différents états du dinar et de la recherche botanique qui a conduit à l’identification des graines. Il s’agit aussi de l’acke, dont la valeur est connue, mais qui reste mystérieux. Tous ces éléments ont fait l’objet d’enquêtes approfondies dont notre bibliographie complète cite les sources. Les rapporter ici aurait compliqué notre démonstration sans rien y ajouter. Elles pourront faire l’objet de communication complémentaire. Elles sont disponibles sur demande.

9) Enfin il apparaît que les poids figuratifs, contrairement à l’opinion de Mollat dont les travaux étaient biaisés par un manque de poids de plus de 80 g, sont aussi précis que les poids géométriques. Nous en avons étudié beaucoup, dont 168 poids de chef ¹⁷, que, pour éviter cette critique, nous n’avons pas utilisés pour nos calculs.

Conclusion

Cette étude prouve, par la seule force du calcul, ce qu’Abel avait pressenti sans pouvoir le prouver. D’abord que le système pondéral des Akan était organisé et précis. Ensuite, qu’il n’était pas basé sur le mitqal, mais sur le taku et le ba, et qu’il était par conséquent d’origine africaine, rendant aux Akan la paternité de cette invention extraordinaire. Enfin, qu’il était composé de poids faibles et de poids forts permettant des échanges à prix constant mais poids variable, bien que sur ce point, l’hétérogénéité de notre échantillon ne nous permette pas d’être aussi affirmatif que sur le reste.

Ce résultat pose finalement bien plus de questions qu’il n’apporte de réponses, car il va nous falloir maintenant expliquer ce qui avait toujours été tenu comme invraisemblable. Comment les Akan ont-ils pu, avec leurs techniques rudimentaires, sans le support de l’écrit, développer, fabriquer et perpétuer, pendant des siècles, dans un espace politique morcelé, un système aussi sophistiqué ?

Nous avions sous les yeux un trésor que nous n’avons pas su voir. Il mérite d’être classé au Patrimoine Mondial de l’Unesco. Les éléments en ont été dispersés avant d’avoir été étudiés en contexte mais nous espérons qu’il reste en Côte d’Ivoire et au Ghana, assez de dja, futuo ou sannaa non adultérés à inventorier pour qu’on puisse en affiner notre compréhension, et déterminer comment les deux sous-systèmes T et T* étaient associés. Ce sera l’occasion de vérifier la reproductibilité de notre théorie par d’autres chercheurs sur d’autres collections.

Bibliographie

Abel A., 1973. Utilisation des poids à peser l'or en Côte d'Ivoire. Journal de la Société́ des Africanistes, 43 : 33-109.

Abel H., 1952-1959. Déchiffrement des poids à peser l'or en Côte d'Ivoire. Journal de la société des Africanistes, 22 (1952) : 95-114 ; 24 (1954) : 7-23 ; 29 (1959) : 273-286.

Binger L. G., 1892. Du Niger au Golfe de Guinée par le pays de Kong et le Mossi. Paris, Hachette, 2 vol. (vol. premier, 513 p. ; vol. second, 414 p.).

Blandin A., 1988. Afrique de l’ouest. Bronzes et autres alliages. Louvain, Balder, 288 p.

Dapper O., 1686. Description de l’Afrique, contenant les Noms, la Situation & les Confins de toutes ses Parties, leurs Rivieres, leurs Villes & leurs Habitations, leurs Plantes & leurs Animaux; les Mœurs, les Coutumes, la Langue, les Richesses, la Religion & le Gouvernement de ses Peuples. Amsterdam, Waesberge, Boom et van Someren, 534 p., 42 pl.

Debien G., Delafosse M. & Thimans G., 1979. Journal d'un voyage de traite en Guinée, à Cayenne et aux Antilles fait par Jean Barbot en 1678-1679. Bulletin de l’Institut fondamental d'Afrique noire, (série B) 40 (2) : 235-395.

Garrard T. F., 1980. Akan weights and the gold trade. Legon history series. London, Longman, 393 p.

Graffenried (von) C., 1992. Goldgewichte akan goldweights. Berne, Benteli, 163 p.

Kjersmeier K., 1948. Ashanti Vægtlodder/Ashanti weights. Copenhagen, Jul Gjellerups Forlag, 23 p.

Menzel B., 1968. Goldgewichte aus Ghana. Berlin, Museum for Völkerkunde, 241 p.

Mollat H., 2003. A new look at the akan gold weights of west Africa. Anthropos, 98 : 31-40.

Niangoran-Bouah G., 1984-1987. L'univers Akan des poids à peser l'or. Dakar, Nouvelles Éditions Africaines, 3 vol. (Vol. I: Les poids non figuratifs, 1984, 316 p. ; vol. II: Les poids figuratifs, 1985, 320 p. ; vol. III: Les poids dans la société, 1987, 328 p.

Nitecki A., 1982. Equal measure for kings and commoners. Goldweight of Ghana Glenbow, Alberta Institute, 69 p.

Ott A., 1968. Akan gold weights. Transactions of the Historical Society of Ghana, 9 : 17-42.

Phillips T., 2010. African goldweights. Miniature sculpture from Ghana. 1400-1900. London, Hansjörg Mayer, 188 p.

Rivallain J., 1989. Poids akans à peser la poudre d'or. Collection Abel. Paris, Direction des monnaies et médailles, 253 p.

Zeller R., 1912. Die goldgewichte von Asante (Westafrika), eine ethnologische Studie. In Baessler-Archiv, 3. Leipzig, Teubner, 77 p.

Other sources

Ahouansou R., Sanya E.A. & Bagan G., 2006. Caractérisation physique et mécanique de la graine de néré (Parkia Biglobosa). Journal de la Recherche Scientifique de l’Université de Lomé, 8 (1): 131-138.

Bohaen A., 1848. Topics in west african history. London, Longman, 174 p.

Bosman W., 1705. A new and accurate description of the coast of Guinea, divided into the Gold, the Slave, and the Ivory coasts. London, Ballantyne Press, 512 p. [Ed. Frank Cass, 1967].

Bouët-Willaumez L.-E., 1848. Commerce et traite des noirs aux côtes occidentales d'Afrique. Paris, Imprimerie Nationale, 230 p.

Bowditch T. E., 1819. Mission from Cape Coast Castle to Ashantee, with a statistical account of that kingdom, and geographical notices of other parts of the Interior of Africa. London, John Murray, 512 p. [Ed. Frank Cass, 1966].

Collectif, 2012-2015. Catalogue des semences forestières. Ouagadougou, Ministère de l’agriculture et du développement durables

De Kolb E., 1968. Ashanti goldweights. New York, Gallery d’Hautbarr, 83 p.

De Marees P., 1605. Description et récit historial du riche royaume d'or de Gunea (sic), aultrement nommé, la coste d'or de Mina, gisante en certain endroict d'Africque. Amsterdam, chez Cornille Claesson, 100 p. [Les éditions Chapitre.com, 2017]

Deveau J. M., 2005. L'or des esclaves. UNESCO, 329 p.

Doursther H., 1840.Dictionnaire universel des poids et mesures anciens et modernes. Bruxelles, Hayez, 603 p.

Garrard T., 1990.Or d'Afrique. Bijoux et parures du Ghana, Côte d'Ivoire, Mali et Sénégal de la collection du Musée Barbier-Mueller. Paris, Hazan, 178 p.

Guilhiermoz P., 1906. Note sur les poids du moyen âge (première partie). Bibliothèque de l'école des chartes, 67 : 161-233.

Lahaderne J.-J.,1981. Dénéraux akan: poids monétaires du XVe au XIXe siècle dans l'Afrique de l'ouest. Arnouville, Arts d'Afrique noire, 200 p.

Meyerowitz E. L. R.,1951. The sacred state of the Akan. London, Faber & Faber, 222 p.

Millogo D., 2014. Étude des caractéristiques morphologiques et de la viabilité des semences de Parkia biglobosa (Jacq.) R. Br. ex G. Don. - Germoplasme de conservation à long terme à 4°C. Burkina Faso, Bobo-Dioulasso, Université Polytechnique de Bobo-Dioulasso, 61 p. (mémoire de fin de cycle, master en gestion et aménagement des écosystèmes forestiers).

Müller W. J.,1676. Die Afrikanische auf der guineischen Gold-Cust gelegene Landschaft Fetu. Hamburg, Zacharias Härtel (3^e ed.)

Olufunke O., Olayode T. & Osuji S., 2016. Emergence of Blighia sapida seeds subjected to different lengths of storage and pretreatments. Journal of Agriculture and Ecology Research International, 6 (1): 1-9. 27.

Pempreh O. N. A, 2008. The history of Ashanti Kings and the whole country itself. Fontes historiae Africanae, New Series. Sources of African history, 6. Oxford University Press, 240 p.

Perrot C.-H., van Dantzig A., 1994. Marie-Joseph Bonnat et les Ashanti-Journal (1869-1874). Coll. Mémoires de la Société des Africanistes. Paris, Société des Africanistes, 672 p.

Prévost d'Exiles A., 1749. Histoire générale des voyages, ou Nouvelle collection de toutes les relations de voyages par mer et par terre, qui ont été publiées jusqu'à présent dans les différentes langues de toutes les nations connues (...). Vol. 17. Paris, Didot, 407 p. (Book 13 & 14).

Rattray R. S., 1923. Ashanti. Oxford, Clarendon press, 348 p.

Rattray R. S., 1927. Religion and art in Ashanti. Oxford, At the Clarendon press, 414 p.

Rømer L. F, 1760. A reliable account of the coast of Guinea. Trans. Selena Axelrod Winsnes. [Oxford University Press, 2000]

Roux C., Guerra M. F., 2000. La monnaie Almoravide: de l’Afrique à l’Espagne. ArchéoSciences, Revue d’Archéométrie, 24 : 39-52.

Les tests statistiques réalisés sur la série des 298 poids de chef pour comparer la théorie dualiste T+T* à celle de Garrard (Mitqal), de Zeller (T*) et Abel (T) ont permis d’obtenir les conclusions suivantes :

Test d’égalité des variances :
Au seuil de risque de 5%, les variances des séries comparées sont significativement différentes (p = 0.0001324). La différence entre les séries n’est donc pas un effet du hasard.

Test de proportion :
Si on définit comme « bonne précision » (BP) les valeurs situées dans la fourchette [-2,4% à +1,5%] autour du standard (pour tenir compte à la fois de la sensibilité des balances, de la précision des fontes et d’une usure liée au temps, minime pour ces gros poids qui ont été moins manipulés que les petites valeurs) et comme « mauvaise précision » (MP) les valeurs qui s’en écartent, le critère de classement devient le pourcentage de poids (par rapport au nombre total de poids) dans chaque catégorie.

Les résultats des tests statistiques sur ce critère dans la classe MP montrent une différence significative au seuil de 5% entre les séries Garrard (58%) et T+T* (11%) [p-valeurs < 2,2 e-16] que le test statistique soit bilatéral (les deux proportions MP sont statistiquement différentes) ou unilatéral (la proportion de MP dans la série T+T* est statistiquement moins élevée au seuil de 5% que celle de la série de Garrard).

Ces tests montrent de la même façon une différence significative au seuil de 5% entre les séries Abel (39%) et T+T* (11%), [p < 8,7 e-15, test bilatéral], et [p < 4,35 e-15, test unilatéral] et les séries Zeller (29%) et  T+T* (11%), [p < 9,91 e-8, bilatéral], et [p < 4,995 e-8, unilatéral].

Au vu de ces résultats on peut affirmer que la théorie dualiste est celle qui décrit le mieux le système pondéral akan.

1. Graine non identifiée à ce stade. ⇧
   

2. Le ba vaut 2 graines d’Abrus precatorius, une liane forestière dont la graine, rouge et noire, est très résistante à la dessiccation. ⇧
   

3. Ces poids, dont la précision est irréaliste avec les techniques dont disposaient les Akan, sont une moyenne qui découle de ses calculs. ⇧
   

4. Designé comme poids mâle et femelle par les Akan. ⇧
   

5. Les Akan l’auraient appris des Arabes par les Dioula, caste de marchands africains islamisés, qui commerçaient avec les deux parties. ⇧
   

6. Mitqal dont la valeur a beaucoup varié au cours des siècles, mais qui n’a jamais officiellement valu 4,4 g. ⇧
   

7. Chez les Akan de l’ouest, dja désigne le trésor dans lequel sont conservés les poids, les instruments de pesée et la poudre d’or. Chez les Akan de l’est on dit futuo pour les trésors familiaux, sannaa pour ceux des états. ⇧
   

8. En excluant, du fait de l’incertitude sur leur rôle pondéral, les poids figuratifs. ⇧
   

9. Données de la littérature : Abel (1973), Blandin (1988), Graffenried (1992), Kjersmeier (1948), Menzel (1968), Nitecki (1982), Phillips (2010) & Rivallain (1989) ; collections de divers musées : British Museum (London), Musée du Quai Branly-Jacques Chirac (Paris), Musée d’ethnographie de Genève [consultées en ligne], Musée d’Angoulême, Musée d’Aquitaine (Bordeaux) & Musée d’histoire naturelle de Toulouse [consultées sur place] ; collections privées : Jean-Jacques Crappier, Pierre Gascou, Gi Mateusen, Tom Phillips, Cemal Pulak, Rainer Sturm & Hans Van der Storm ; et vendeurs spécialisés. ⇧
   

10. Ainsi un poids de 142 g qui vaut soit 568 T* soit 645 T est classé dans la case 640 de préférence à la case 576 dont il est plus éloigné. (+1% versus – 1,4%). ⇧
    

11. Respectivement 2,88/2, 2,8/2 et 3,3/2. ⇧
    

12. Étape première de la fabrication d’une sauce appelée Soumbala en Côte d’Ivoire, dawa-dawa au Ghana. ⇧
    

13. Données vérifiées par l’auteur sur des graines provenant de la région. ⇧
    

14. Idem. ⇧
    

15. Ce n’est que plus tard, à la suite d’une baisse de qualité de l’or akan, que la £ s’est trouvée en phase avec le système faible. ⇧
    

16. L’acke était utilisé couramment dans la traite en Gold Coast. Sa version légère pèse 1,76 g, la lourde 2 g. ⇧
    

17. 90% de ces 168 poids de chefs s’inscrivent dans la fourchette étroite. ⇧
    

Auteur correspondant : J.-J. Crappier

Jean-Jacques Crappier
Collectionneur, Le Mans, France
Email : Cette adresse e-mail est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser. 

Christian Farinetto
PhD, Laboratoire de Mathématiques, Le Mans Université, France

Pierre Gascou
Ingénieur, collectionneur, Versailles, France

Carole Maunoury
Economiste. Statesia, Le Mans, France

Franck Maunoury
PhD, Statisticien et économiste. Statesia, Le Mans, France

Gi Mateusen
Journaliste & producteur, collectionneur. Turnhout, Belgique