The Akan Weighing System restored after 120 years of oblivion. A metrological study of 9301 geometric gold-weights
Le Système pondéral Akan reconstitué après 120 ans d’oubli. Une étude métrologique de 9301 poids géométriques à peser l’or
- Jean-Jacques Crappier, Christian Farinetto, Pierre Gascou, Carole Maunoury, Franck Maunoury & Gi Mateusen
|
Precise, sophisticated, complicated but functional, this weighing system, used by the Akan until their colonization to pay in gold powder, has been little studied by ethnologists. One must say that its complexity did not encourage much interest, especially since the discussion seemed to have been closed in 1980 by Timothy Garrard, for whom the Akan had learned their weighing system from the Arabs by the Dioula, caste of African merchants who traded with both sides in the context of the trans-Saharan trade. The study of a series of 9,301 weights, including 298 weights over 80 g, contradicts this theory in favor of an aboriginal system, based on seeds and rigorously structured, in which exchanges were probably made thanks to a double set of light and heavy weights allowing transactions at constant price but variable weight. The high level of proof of this metrological study questions the way in which the Akan were able, with rudimentary techniques, to develop, perpetuate and transmit, orally, for centuries, in a fragmented political space, such a sophisticated system? Keywords: African Currencies - Goldweights - Gold Weight - Weighing System - Akan - Ashanti - Baule - Abel Henri - Garrard Timothy - Ba - Taku Précis, sophistiqué, compliqué mais fonctionnel, ce système de poids africains, utilisé par les Akan jusqu’à leur colonisation pour payer en poudre d’or, est totalement passé sous les radars de la recherche ethnographique. Il faut dire que sa complexité n’encourageait guère à s’y intéresser, d’autant que l’affaire semblait résolue depuis 1980 par Timothy Garrard pour qui les Akan l’avaient appris des Arabes par les Dioula, caste de marchands africains islamisés, qui commerçaient avec les deux parties dans le cadre de la traite transsaharienne. L’étude d’une série de 9301 poids, dont 298 poids de plus de 80 g, vient contredire cette théorie au profit de celle d’un système autochtone, basé sur des graines et rigoureusement structuré, dans lequel les échanges se faisaient vraisemblablement grâce à un double jeu de poids faibles et de poids forts, permettant des transactions à prix constant mais poids variable. Le fort niveau de preuve de cette étude métrologique pose le problème de savoir comment les Akan ont pu, avec des techniques rudimentaires, développer, perpétuer et transmettre oralement, pendant des siècles, dans un espace politique morcelé, un système aussi sophistiqué ? Mots clés : Monnaies africaines - protomonnaies - poids à peser l’or - système pondéral - Akan - Ashanti - Baoulé - Abel Henri - Garrard Timothy - Ba - Taku |
Sorting of the 298 Chiefs’ Weights in taku
Sorting the Chiefs’ Weights. Garrard versus dualistic hypothesis
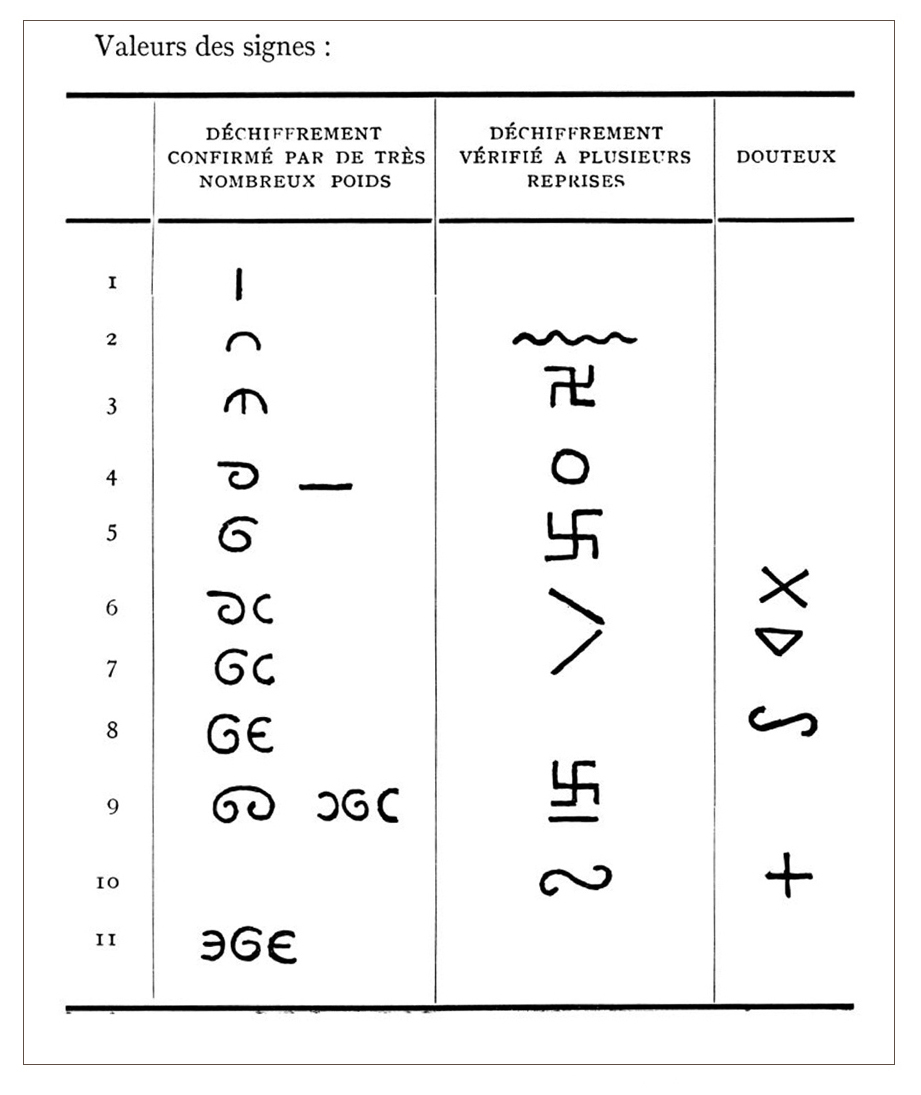
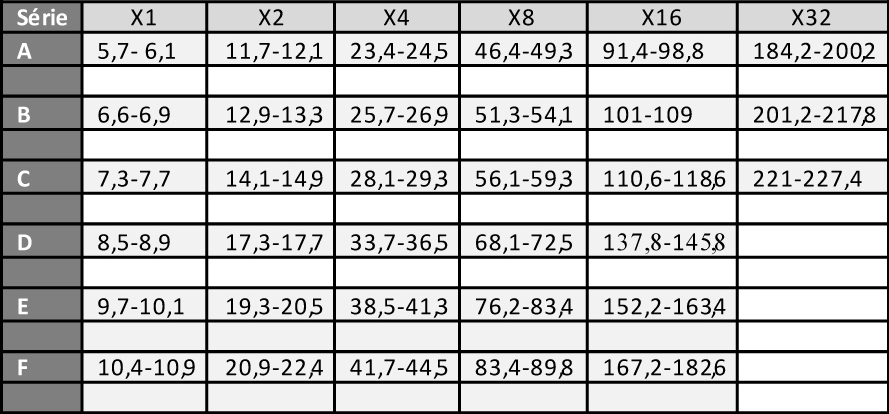
Figurative or geometric, theses weights have been little studied by scholars and their meaning remains mysterious, although we have information gathered by generations of merchants and explorers and thousands of weights in museums and individual collections. A few searchers have tried to unravel its mystery from ancient descriptions, field data and metrological studies. Rudolph Zeller, the first, described in 1912 (Zeller, 1912), from information collected in Ghana, a system based on the taku 1, a seed weighing 0.25 g. Very complex, it is organized in 7 parallel series whose first values are 1,3,5,7, 9, 11 and 13 taku, and whose following are a succession of multiples by 2, that is to say 4,8,16,32 to 512 and beyond. These works are taken up in 1952 by Henri Abel, in Ivory Coast, who introduces a second grain unit, the ba 2, with a calculated weight of 0.146 g, in a ratio of 3 to 2 with the taku, the weight of which he reevaluates at 0.22 g (Abel, 1952) 3. He also introduces the notion of a dual system, combining “male and female” weights 4, allowing transactions at constant price but variable weight, in which you sell what you paid in gold at the same price, but in lesser quantities, the difference representing your profit, or your interest in the case of a loan. Moreover, Abel, convinced that the signs decorating the weights had a numerical value, had proposed a grid to decipher them (Fig. 1).
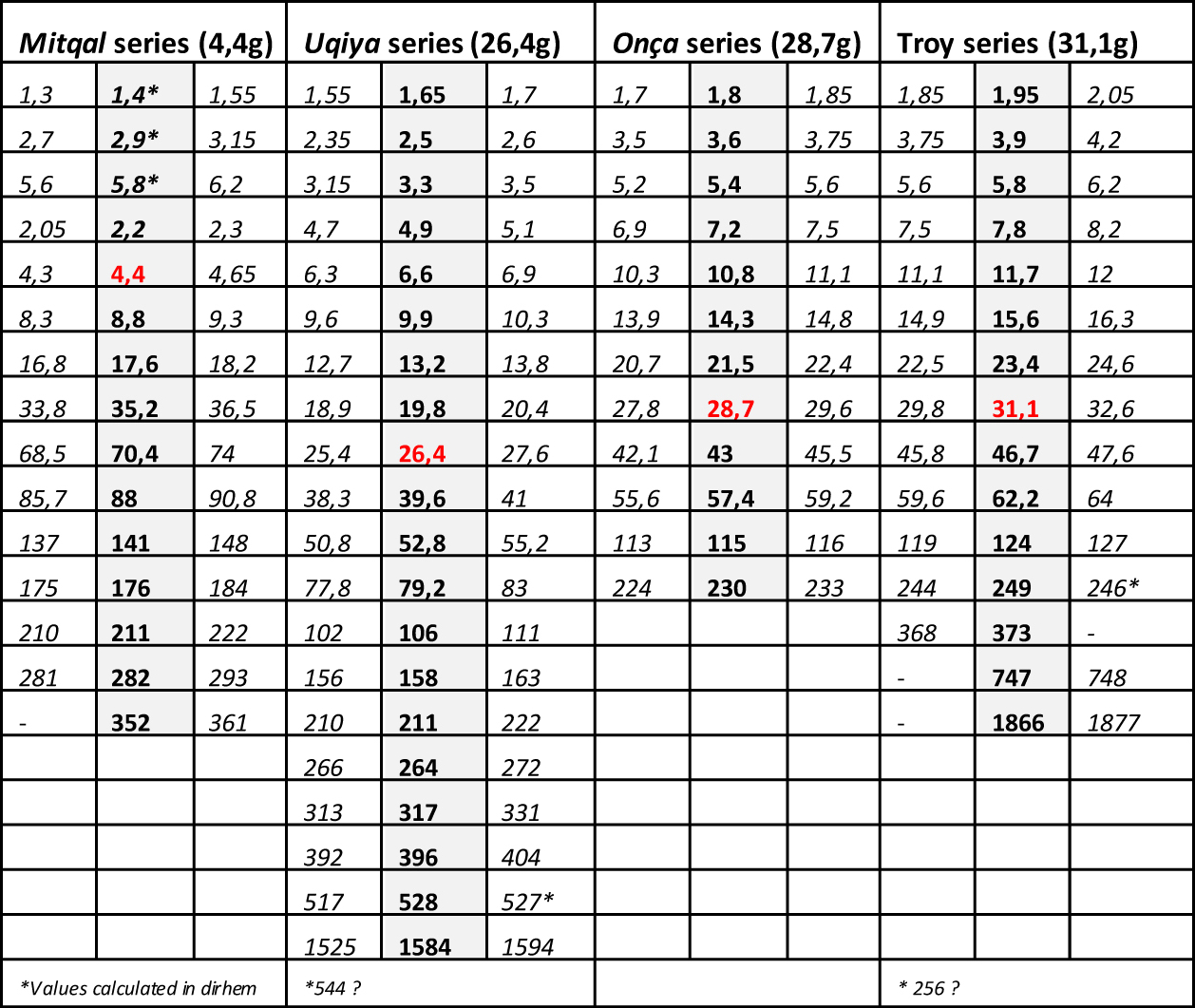
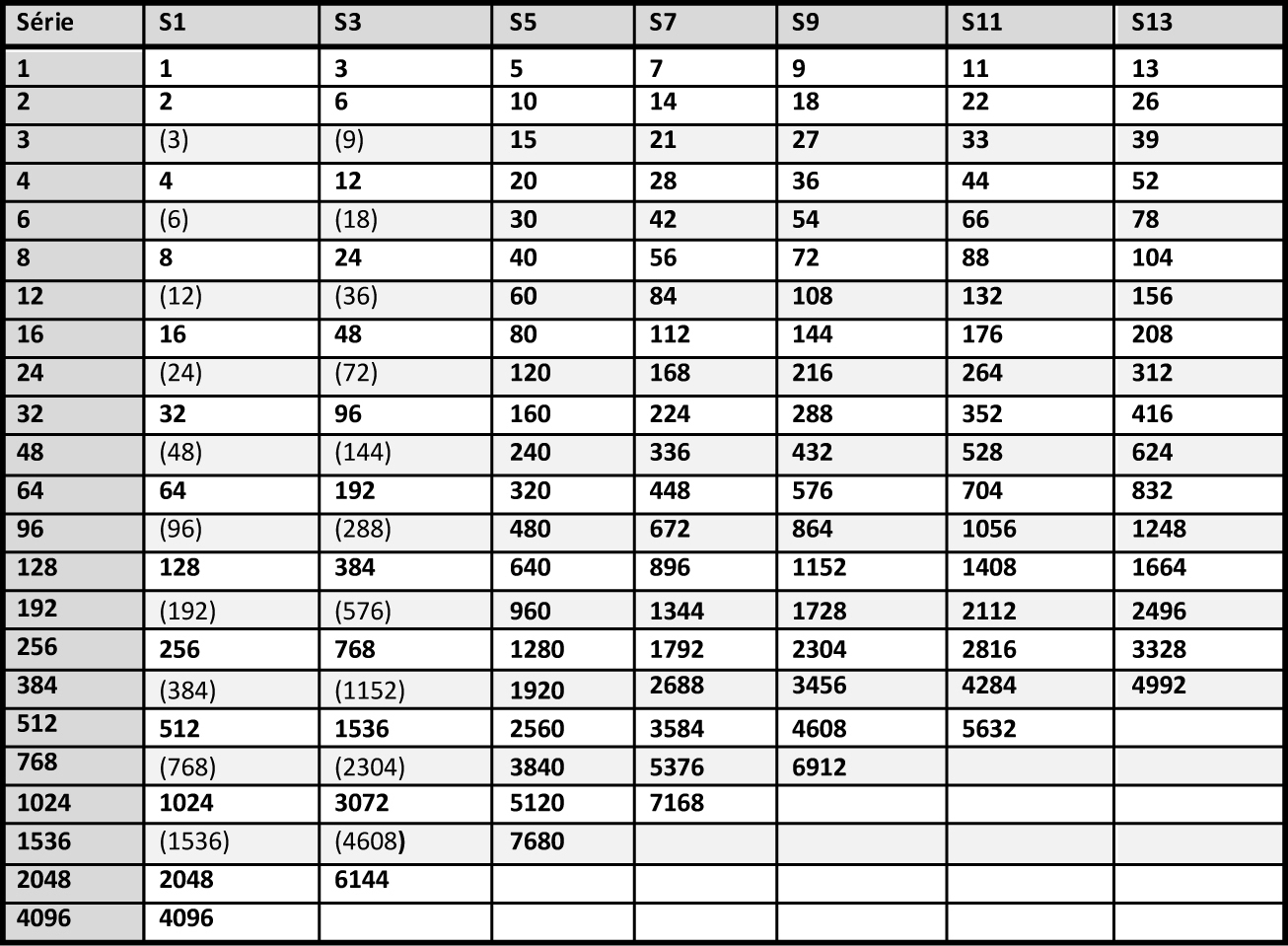
In 1987, Georges Niangoran-Bouah, Ivorian ethnologist, supports as Abel the thesis of a dual system, which he says still in force at that time on the markets of Abidjan, but without going further in the demonstration (Niangoran-Bouah, 1987). In 2003, Harmut Mollat, with a study of 3800 weights (Mollat, 2003), partially questions Garrard's thesis, challenging the materiality of the series of European origin and the weighing role of the figurative weights, but keeping to the mitqal his central role, and to taku, just like Garrard, a marginal role, with the weight of 0.25 g. But Garrard's theory, even corrected by Mollat, is not consistent with the weight lists he reports himself in his book. Collected in the different Akan states from elderly notables, established in English currency, none quotes the mitqal but all report taku, valued at 6p, which, in 8.8 g of gold akan for £, quoted by same informants, gives him the weight of 0.22 g. Garrard did not consider these lists in his demonstration. It is for us the origin of his error, and an indication that the weight of 4.4 g, which is the cornerstone of his theory, is not an africanized mitqal 6, but the counter-value of 10 shilling, and the twentyfold of taku of Abel, whose existence is thus confirmed. Dualistic hypothesis: By compiling the weight lists left to us by European merchants as early as the 16th century, by deconstructing the structure of their Akan appellations, we build, on Zeller's model, the framework of this system, in the form of a complex multiplication table (Table 2). It has about a hundred boxes, corresponding to the Zeller multiplicands (1,3,5,7,9,11 and 13) multi-folded by 2,4,8,16 and so on, but also 3,6,12,24 and so on. Refer to Table 2 for visualization.
However, we must also consider a more trivial hypothesis that would make this apparent complexity the consequence, over centuries and exchanges, of the interweaving of regional or even familial systems, in which only a few weights, more or less based on the mitqal and known only to their owners, would have been really used as weight, the other parts of the dja 7 being worth more by their magical or symbolic value. |
|
To study the Akan Weighing System, we have collected 9301 geometric weights 8 from various sources 9, ranging from 1,3 g to 1900 g, of which 2420 weigh 20 to 80 g and 298 more than 80 g. Despite the heterogeneity of this set we want to show: If we have seen right: 1) All weights, after transformation into the corresponding light or heavy system, must fit into one of the multiplication table boxes with, according to experiments conducted on akan scales, a minimum accuracy of ± 2%, in practice [-2,5% to + 1.5%], due to wear. The number of weights within this narrow range will be our endpoint to validate the Akan multiplication table. 2) Garrard's theory should fail to describe our set with such precision. As well as those of Abel and Zeller. This will be our endpoint to validate dualistic theory.
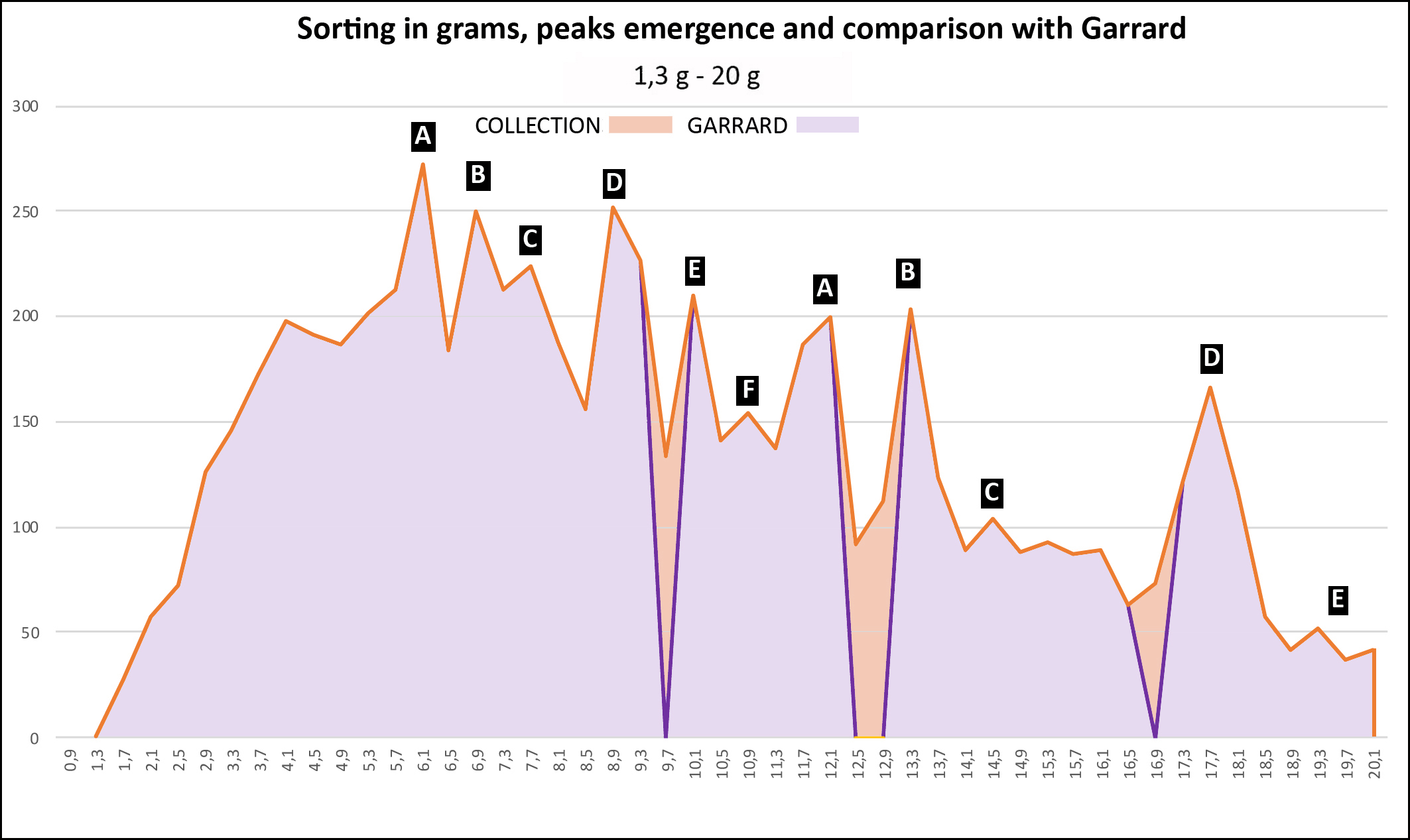
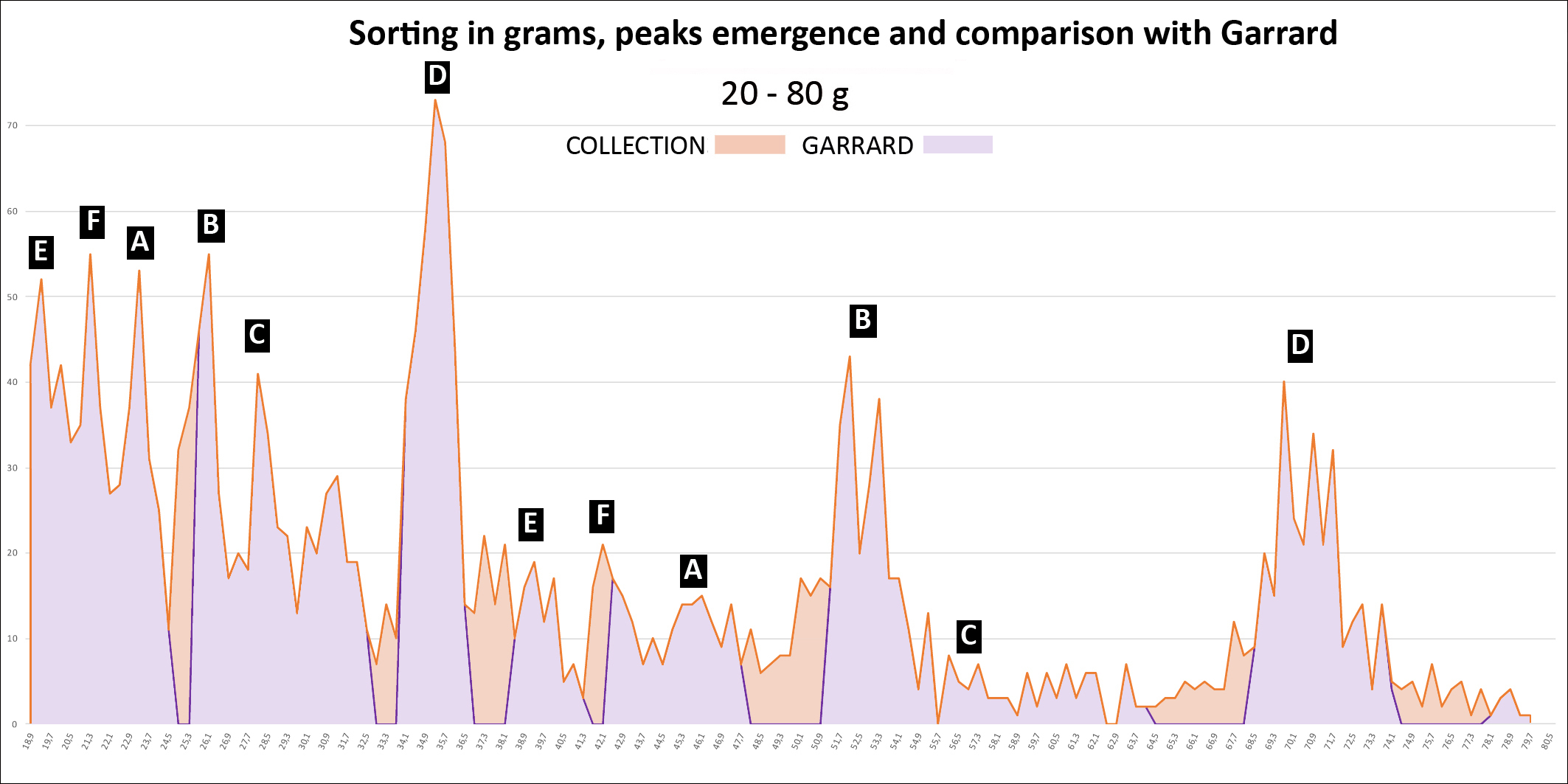
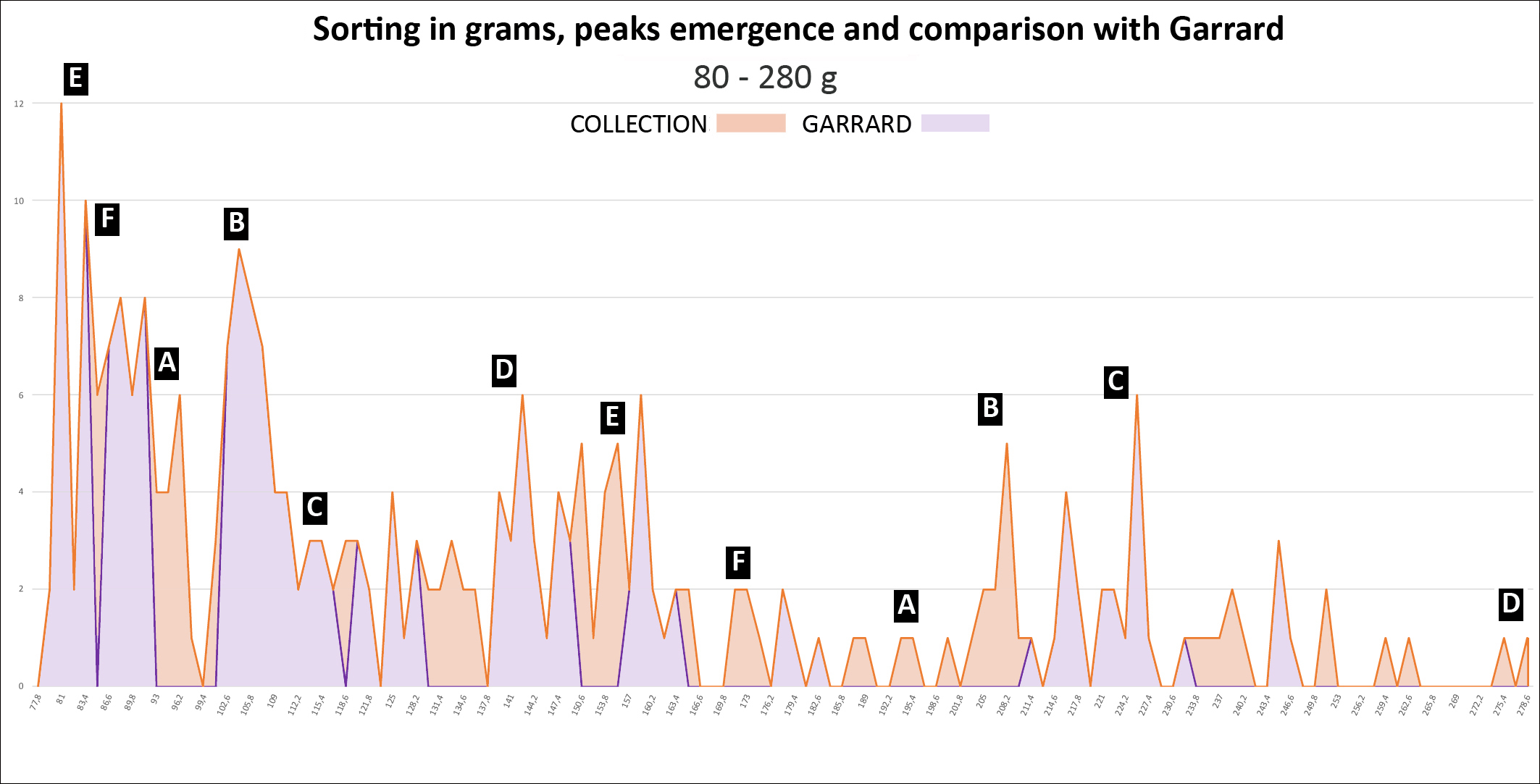
We treated our set with an Excel spreadsheet: 1) Sorting in grams: 2) Sorting in taku:
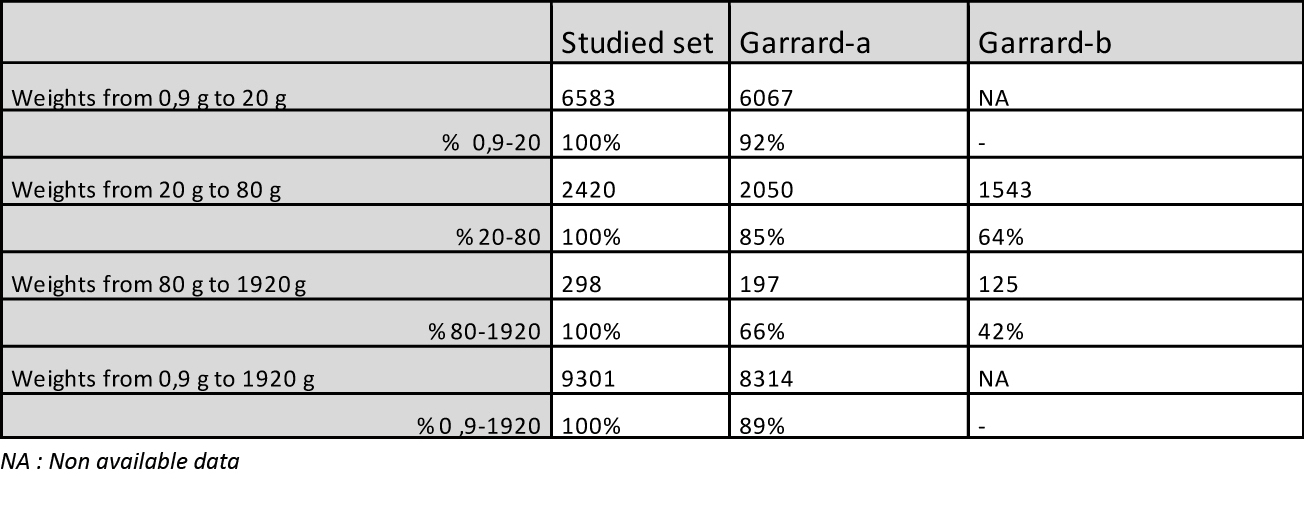
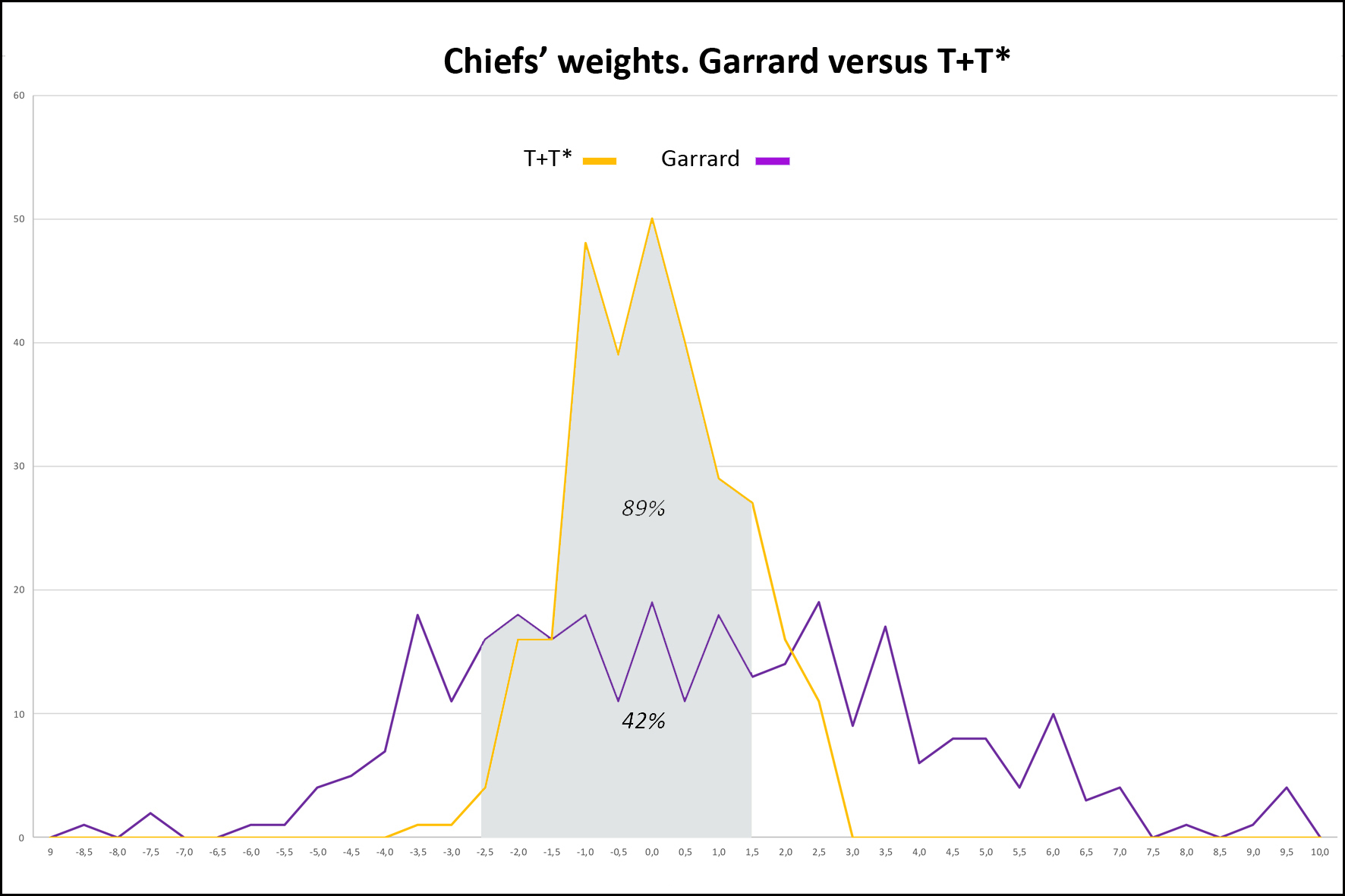
Weight distribution: - From 6 g peaks are individualized in an apparent disorder from which emerge at least 6 successive series, noted from A to F, each following a geometric progression of reason 2 whose scheduling is detailed in Table 3. The B and D series correspond to Garrard’s uqiya and mitqal series values (see Table 1). - The graphs also show how weights should be distributed if they were following Garrard's theory, according to his sorting classes (purple line). The first gaps appear from 9.3 g. They are visualized on the graphs by the areas in light orange. - The Table 4 shows that while Garrard's theory accounts for 89% of weights overall, between 20 and 80 g this score drops to 85% (2050/2420) and 66% above 80 g (197/298) (Garrard-a column). Considering the narrow range (Garrard-b column), it drops to 64% (1543/2420) and 42% (125/298).
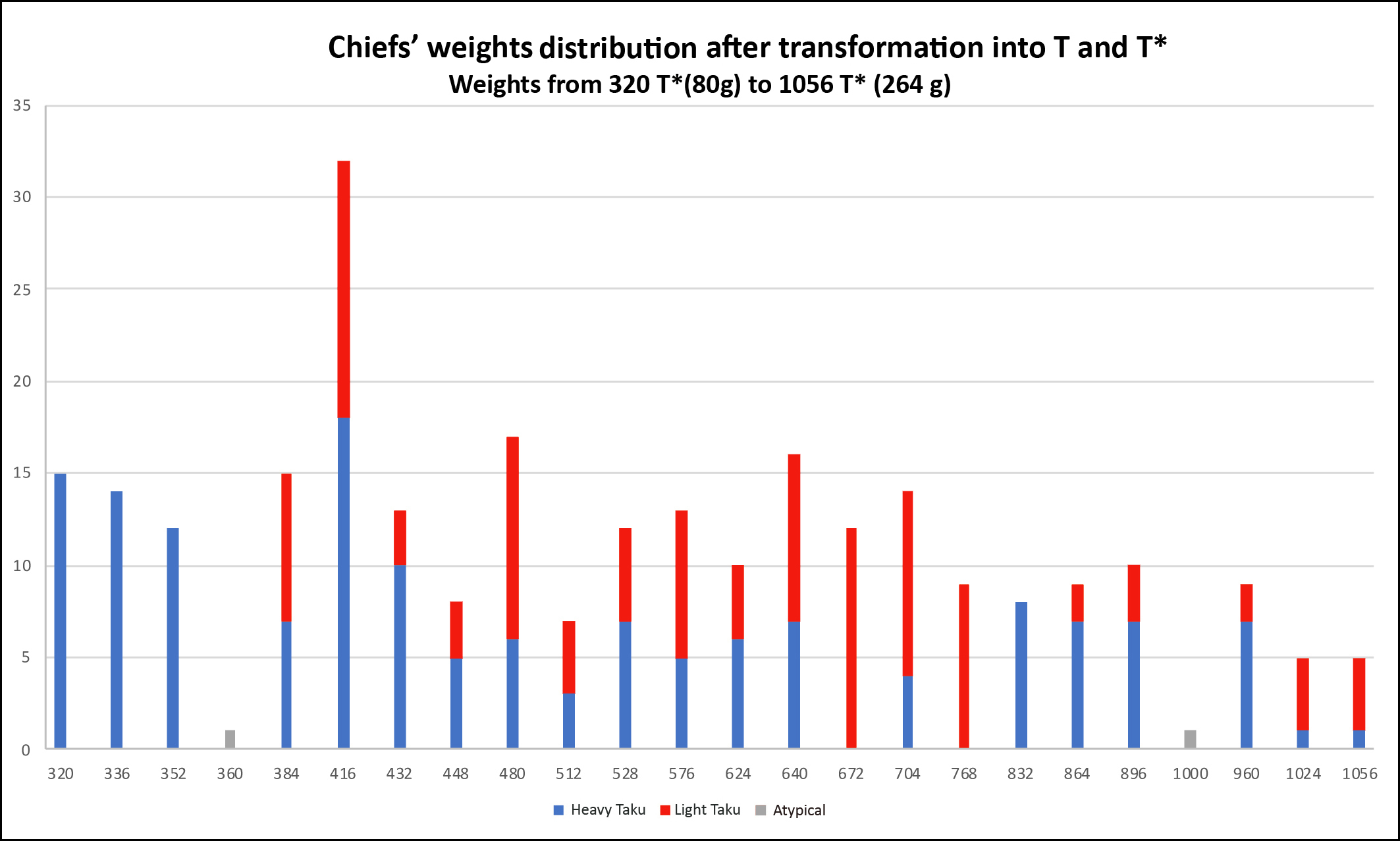
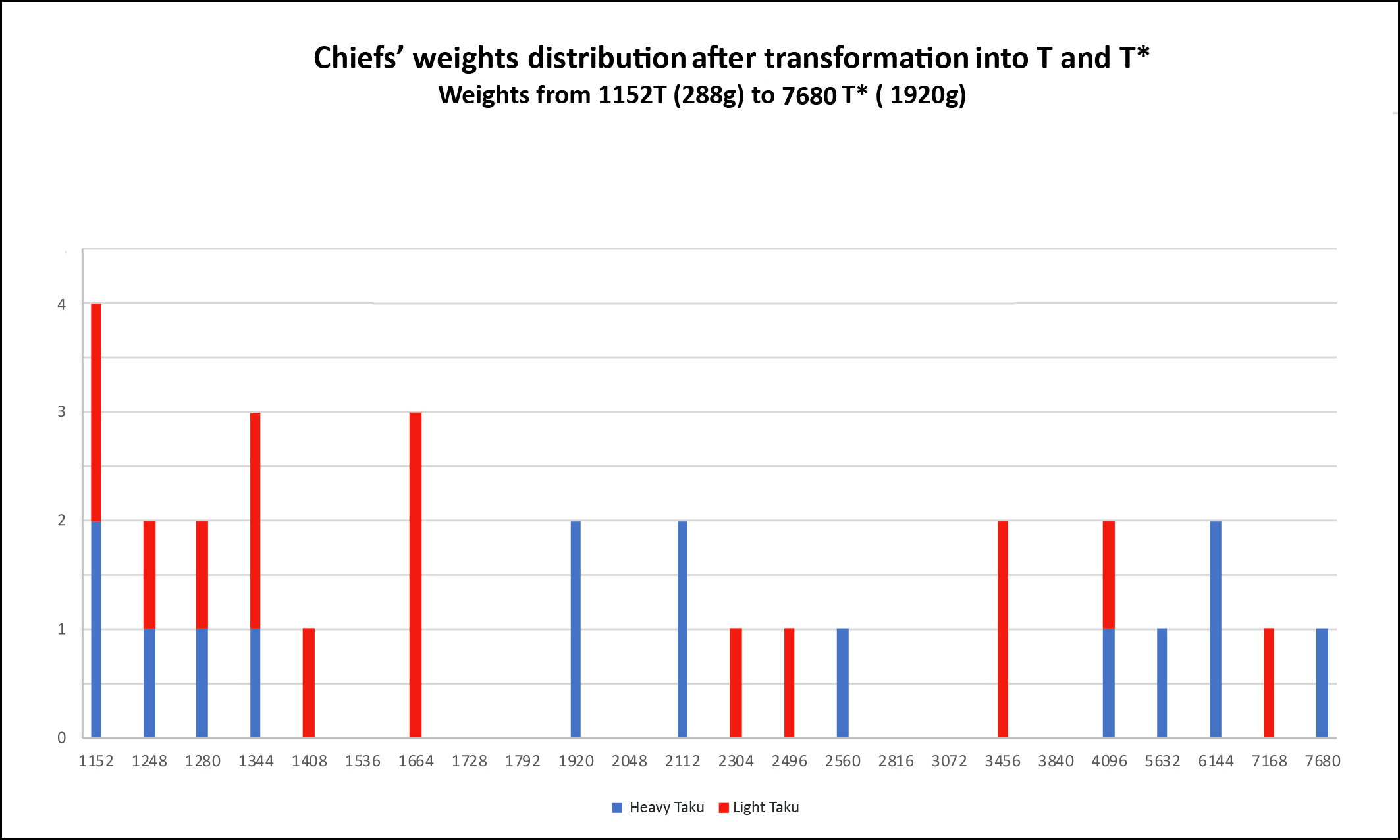
2) Sorting of the 298 Chiefs’ Weights in taku All calculations were done in taku for reasons that we previously discussed. - Figures 5 and 6 report their sorting in taku as a stacked histogram. Transformed in T or T*, all Chiefs’ Weights, but two, find their place in the multiplication table.
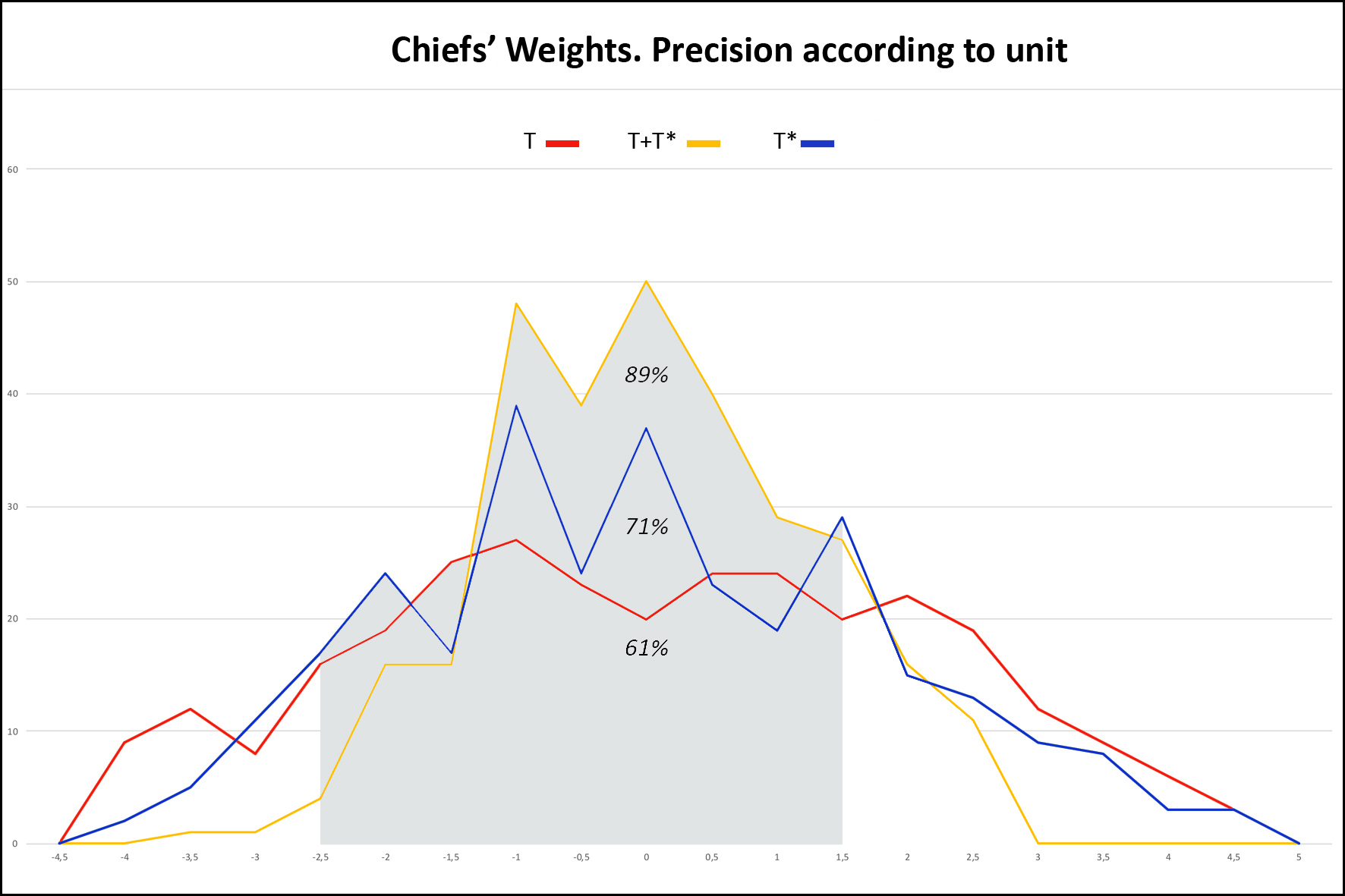
3) Sorting the Chiefs’ Weights. Garrard versus dualistic hypothesis Figure 8 confronts the precision that Garrard's grid allows with that of the dualistic hypothesis. The Garrard curve ranges from [-9% to + 10%]. We find the 125 weights (42%) of Table 4 corresponding to the narrow range. 91 of these 125 weights (73%) belong to the mitqal or uqiya series, 18 (14%) and 16 (13%) to the so-called Portuguese and English series.
1) What about our collection? This is the largest collection of geometric weights ever studied, whose strong point are the 298 Chiefs’ Weights. Garrard had gathered only 2000, and Mollat 2500, with very few values >80g. Composed of weights of all ages and from diverse origins it shows the uniqueness of the Akan Weighing System in time and space. Far from anarchy, it shows its rigorous organization, in the form of series of peaks that can be interpreted as a succession of Gauss curves around a pivot value, but also, in view of their progressive growth, like composite sets, associating values in T and T*. 2) Is the result of Chiefs’ Weights sorting validating Akan multiplication table ? The sorting result in the T + T* system is unequivocal with a score of 89%, rising to 94% if we tolerate a higher margin ≤2%. Given the avatars that some of these weights have experienced, that the sometimes-poor quality of our photographic documentation does not always identify, and the possibility that some false have slipped in, we can speak of "almost 100%". Our first end point is therefore fulfilled. These results validate the Akan multiplication table with its consequences on Akan people's arithmetic skills. 3) Which of the four theories is favored by the comparison of precisions? 89% accuracy for T + T* versus 71% for T* and 61% for T (Figure 7), statistical tests (see Annex) proving that these differences are significant, we can say that the dualistic theory better accounts for the distribution of Chiefs’ Weights than the Zeller and Abel theories. For these last two, the large number of imprecise weights located at the extremes of the curve is the sign that they belong to the other category. Garrard's theory is the one that that gives the worst description of our collection, whose sorting in grams shows that it diverges all the more from the reality that it progresses in weight and precision. We note that if the B and D series correspond respectively to Garrard’s uqiya and mitqal series, they correspond as well to multiples by 3,6,12 and so on, and 2,4,8 and so of the light taku (see Table 2). With only 125 weights (42%) in the narrow range [-2.5% to 1.5%], it is also the theory whose accuracy is the worst when faced with Chiefs’ Weights. Moreover, the analysis of these 125 weights shows that 73% belong to the Islamic series and 14% to the Portuguese series, both falling under the weak system. So, we might say that it is a kind of degraded light taku theory. Our second end point is thus satisfied, which validates the duality of weights, but the heterogeneity in time and space our set does not allow us to affirm that it is a dualistic integrated system rather than two systems, one in T and one in T*, geographically separated. Prematurely deceased, Garrard cannot answer our critics. How to explain this error despite his erudition and the relevance of his historical analysis? We see here the consequence of its informants’ acculturation, who, although very old, had probably never used the weights themselves, or in a system already degraded and subservient to British weights and currencies, in which transactions were, at this time, made in the light system. They did not know, or had forgotten, all the subtilties, these stories of male and female weight, or the role of the seeds. Garrard's theory explained, by barely forcing, 90% of the weight; Zeller's was incomplete; Abel's was confused; 20 T are very close to mitqal; he did not have the computer tools to manipulate his collection or enough Chiefs’ Weights to understand that his theory did not explain them. For what reason would he have questioned the correctness of his theory? 4) What are the seeds without which the Akan Weighing System could not work? Only the seed corresponding to the light ba is known. Taku has kept its mystery, but a search on Google with, by analogy, "carob tree" as a keyword, leads us to nere, the African carob tree, aka Parkia biglobosa, whose seed is consumed by the Akan. With an average of 0.25 g, it weighs only 0.22 g 12, once boiled and then peeled 13, making it a very suitable taku. In the case of Abrus precatorius, the solution comes from Abel, who tells us that, depending on whether it is harvested during the dry or wet season, the average weight of the seed, which takes 2 to make a ba, is 74 mg or 83 mg 14. 5) How then to explain that the European merchants did not understand this dualism? Presumably by the flexibility of Akan weights, which, by a chance effect, the light system was in phase with the Arab and Portuguese weights, while the heavy system was paired with that of the Dutch and then the English 15. The Akan, who checked each transaction with their own weight, therefore used one or the other system according to their interlocutor, who could only know the part that concerned him. Everybody was not unaware of this duality, since Dapper (1686) and Barbot (1679 as cited in Debien et al., 1979) have, more or less explicitly, established. 6) Can such a precision be attributed to a system considered as empirical and of magical essence? The reality of numbers is there which proves the high degree of organization and precision of the Akan system. We are not in the field of ethnology, but in that of metrology. Astonishing as it may be, Akan have come to calculate complex operations without written support, and to manufacture weights with almost industrial precision. It is for the experts to explain how. 7) Deliberately we did not write about decoding the weights that Abel believed possible without being able to prove it. Our experience, however, has shown us that with some modifications of its grid, the possibility of calculating in one or the other of the two systems in ba and taku, and the introduction for the heaviest weights of the acke, a third unit with a value of 8 taku 16, it was possible to decode more than 50% of the weights, in a relatively standardized way and by scrupulously respecting the values of the multiplication table. It has been possible for half of the Chiefs’ Weights, and a better photographic documentation would have improved this score. 8) In this presentation, some points are assumed pre-acquired, or are briefly summarized. This is the way in which the Akan multiplication table was established, historical documents that support the hypothesis of a dualistic system, variations of the dinar over the centuries and botanical research that led to the identification of seeds. It is also the case of the acke, whose value is known, but which remains rather mysterious. These elements have been extensively investigated and our full bibliography cites the sources. Reporting them would have complicated our demonstration without adding anything to it. They may be the subject of further communication. They are available on request. 9) We will conclude by saying that the figurative weights, contrary to the opinion of Mollat whose series lacked weight of more than 80 g, are as precise as the geometric ones. We studied a lot of them, including 168 Chiefs’ Weights 17, which, to avoid this criticism, we did not use for our calculations. |
|
This study proves, by the mere force of calculation, what Abel had foreseen without being able to prove it. First, the Akan Weighing System was organized and accurate. Then, that it was not based on mitqal, but on taku and ba, and therefore was of African origin, giving back to the Akan people the paternity of this extraordinary invention. Third, that it was composed of light and heavy weights allowing trade at constant price but variable weight, although on this point, the heterogeneity of our sample does not allow us to be as positive as on the rest. But this result finally raises many more questions than it answers, because we will now have to explain what had always been considered as improbable. How could these people, with their rudimentary techniques, without the support of writing, develop, fabricate and perpetuate, for centuries, in a fragmented political space, such a sophisticated system? We had before us a treasure that we have not seen. It deserves to be listed on the UNESCO World Heritage List. Many elements have been dispersed before being studied in their context, but we hope there remains, in Ivory Coast and Ghana, enough unadulterated dja, futuo and sannaa to inventory so that we can refine our understanding and determine how the two subsystems T and T * were associated. This will be an opportunity for other researchers to verify our theory on other collections. |
|
Abel A., 1973. Utilisation des poids à peser l'or en Côte d'Ivoire. Journal de la Société́ des Africanistes, 43: 33-109. Abel H., 1952-1959. Déchiffrement des poids à peser l'or en Côte d'Ivoire. Journal de la société des Africanistes, 22 (1952): 95-114 ; 24 (1954): 7-23 ; 29 (1959): 273-286. Binger L. G., 1892. Du Niger au Golfe de Guinée par le pays de Kong et le Mossi. Paris, Hachette, 2 vol. (vol. premier, 513 p. ; vol. second, 414 p.). Blandin A., 1988. Afrique de l’ouest. Bronzes et autres alliages. Louvain, Balder, 288 p. Dapper O., 1686. Description de l’Afrique, contenant les Noms, la Situation & les Confins de toutes ses Parties, leurs Rivieres, leurs Villes & leurs Habitations, leurs Plantes & leurs Animaux; les Mœurs, les Coutumes, la Langue, les Richesses, la Religion & le Gouvernement de ses Peuples. Amsterdam, Waesberge, Boom et van Someren, 534 p., 42 pl. Debien G., Delafosse M. & Thimans G., 1979. Journal d'un voyage de traite en Guinée, à Cayenne et aux Antilles fait par Jean Barbot en 1678-1679. Bulletin de l’Institut fondamental d'Afrique noire, (série B) 40(2): 235-395. Garrard T. F., 1980. Akan weights and the gold trade. Legon history series. London, Longman, 393 p. Graffenried (von) C., 1992. Goldgewichte akan goldweights. Berne, Benteli, 163 p. Kjersmeier K., 1948. Ashanti Vægtlodder/Ashanti weights. Copenhagen, Jul Gjellerups Forlag, 23 p. Menzel B., 1968. Goldgewichte aus Ghana. Berlin, Museum for Völkerkunde, 241 p. Mollat H., 2003. A new look at the akan gold weights of west Africa. Anthropos, 98: 31-40. Niangoran-Bouah G., 1984-1987. L'univers Akan des poids à peser l'or. Dakar, Nouvelles Éditions Africaines, 3 vol. (Vol. I: Les poids non figuratifs, 1984, 316 p. ; vol. II: Les poids figuratifs, 1985, 320 p. ; vol. III: Les poids dans la société, 1987, 328 p. Nitecki A., 1982. Equal measure for kings and commoners. Goldweight of Ghana Glenbow, Alberta Institute, 69 p. Ott A., 1968. Akan gold weights. Transactions of the Historical Society of Ghana, 9: 17-42. Phillips T., 2010. African goldweights. Miniature sculpture from Ghana. 1400-1900. London, Hansjörg Mayer, 188 p. Rivallain J., 1989. Poids akans à peser la poudre d'or. Collection Abel. Paris, Direction des monnaies et médailles, 253 p. Zeller R., 1912. Die goldgewichte von Asante (Westafrika), eine ethnologische Studie. In Baessler-Archiv, 3. Leipzig, Teubner, 77 p. Other sources Ahouansou R., Sanya E.A. & Bagan G., 2006. Caractérisation physique et mécanique de la graine de néré (Parkia Biglobosa). Journal de la Recherche Scientifique de l’Université de Lomé, 8(1): 131-138. Bohaen A., 1848. Topics in west african history. London, Longman, 174 p. Bosman W., 1705. A new and accurate description of the coast of Guinea, divided into the Gold, the Slave, and the Ivory coasts. London, Ballantyne Press, 512 p. [Ed. Frank Cass, 1967]. Bouët-Willaumez L.-E., 1848. Commerce et traite des noirs aux côtes occidentales d'Afrique. Paris, Imprimerie Nationale, 230 p. Bowditch T. E., 1819. Mission from Cape Coast Castle to Ashantee, with a statistical account of that kingdom, and geographical notices of other parts of the Interior of Africa. London, John Murray, 512 p. [Ed. Frank Cass, 1966]. Collectif, 2012-2015. Catalogue des semences forestières. Ouagadougou, Ministère de l’agriculture et du développement durables. De Kolb E., 1968. Ashanti goldweights. New York, Gallery d’Hautbarr, 83 p. De Marees P., 1605. Description et récit historial du riche royaume d'or de Gunea (sic), aultrement nommé, la coste d'or de Mina, gisante en certain endroict d'Africque. Amsterdam, chez Cornille Claesson, 100 p. [Les éditions Chapitre.com, 2017] Deveau J. M., 2005. L'or des esclaves. UNESCO, 329 p. Doursther H., 1840.Dictionnaire universel des poids et mesures anciens et modernes. Bruxelles, Hayez, 603 p. Garrard T., 1990.Or d'Afrique. Bijoux et parures du Ghana, Côte d'Ivoire, Mali et Sénégal de la collection du Musée Barbier-Mueller. Paris, Hazan, 178 p. Guilhiermoz P., 1906. Note sur les poids du moyen âge (première partie). Bibliothèque de l'école des chartes, 67: 161-233. Lahaderne J.-J.,1981. Dénéraux akan: poids monétaires du XVe au XIXe siècle dans l'Afrique de l'ouest. Arnouville, Arts d'Afrique noire, 200 p. Meyerowitz E. L. R.,1951. The sacred state of the Akan. London, Faber & Faber, 222 p. Millogo D., 2014. Étude des caractéristiques morphologiques et de la viabilité des semences de Parkia biglobosa (Jacq.) R. Br. ex G. Don. - Germoplasme de conservation à long terme à 4°C. Burkina Faso, Bobo-Dioulasso, Université Polytechnique de Bobo-Dioulasso, 61 p. (mémoire de fin de cycle, master en gestion et aménagement des écosystèmes forestiers). Müller W. J.,1676. Die Afrikanische auf der guineischen Gold-Cust gelegene Landschaft Fetu. Hamburg, Zacharias Härtel (3e ed.) Olufunke O., Olayode T. & Osuji S., 2016. Emergence of Blighia sapida seeds subjected to different lengths of storage and pretreatments. Journal of Agriculture and Ecology Research International, 6(1): 1-9. 27. Pempreh O. N. A, 2008. The history of Ashanti Kings and the whole country itself. Fontes historiae Africanae, New Series. Sources of African history, 6. Oxford University Press, 240 p. Perrot C.-H., van Dantzig A., 1994. Marie-Joseph Bonnat et les Ashanti-Journal (1869-1874). Coll. Mémoires de la Société des Africanistes. Paris, Société des Africanistes, 672 p. Prévost d'Exiles A., 1749. Histoire générale des voyages, ou Nouvelle collection de toutes les relations de voyages par mer et par terre, qui ont été publiées jusqu'à présent dans les différentes langues de toutes les nations connues (...). Vol. 17. Paris, Didot, 407 p. (Book 13 & 14). Rattray R. S., 1923. Ashanti. Oxford, Clarendon press, 348 p. Rattray R. S., 1927. Religion and art in Ashanti. Oxford, At the Clarendon press, 414 p. Rømer L. F, 1760. A reliable account of the coast of Guinea. Trans. Selena Axelrod Winsnes. [Oxford University Press, 2000] Roux C., Guerra M. F., 2000. La monnaie Almoravide: de l’Afrique à l’Espagne. ArchéoSciences, Revue d’Archéométrie, 24: 39-52. |
|
Statistical tests performed on the 298 Chief’s Weights series to compare the dual T + T * theory with that of Garrard (Mitqal), Zeller (T *) and Abel (T) yielded the following conclusions: Test to compare variances: Test for equality of proportion: The results of the statistical tests on this criterion in the PP class show a significant difference at the 5% threshold between the Garrard series (58%) and the T + T * series (11%) [p-values <2.2 e-16] whether the statistical test is bilateral (the two proportions PP are statistically different) or unilateral (the proportion of PP in the T + T * series is statistically lower at the 5% threshold than that of the Garrard series). These tests similarly show a significant difference at the 5% threshold between the Abel series (39%) and T + T * series (11%), [p <8.7 e-15, bilateral test], and [p <4.35 e-15, one-sided test] and the Zeller series (29%) and T + T * series (11%), [p <9.91 e-8, bilateral], and [p <4.995 e-8, unilateral]. These results allow us to affirm that the dualistic theory is the one that best describes the Akan Weighing System.
|
|
|
Corresponding author: J.-J. Crappier Jean-Jacques Crappier Christian Farinetto Pierre Gascou Carole Maunoury Franck Maunoury Gi Mateusen |
| Crappier J.-J., Farinetto C., Gascou P., Maunoury C., Maunoury F. & Mateusen G., 2019. The Akan Weighing System restored after 120 years of oblivion. A metrological study of 9301 geometric gold-weights. Colligo, 2(2). |